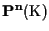
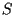
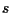
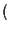
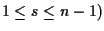
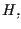
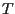
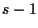
8 ESERCIZIO   Dimostrare che in uno spazio proiettivo $\mathbf{P^n} (\mathrm{K})$ un sottospazio proiettivo $S$ di dimensione $s$ $($con $1 \leq s \leq n-1)$ o è contenuto in un iperpiano proiettivo $H,$ oppure ha con esso un sottospazio proiettivo $T$ di dimensione $s-1$ in comune.
In particolare: una retta proiettiva o è contenuta in un iperpiano proiettivo, oppure lo interseca in un unico punto.

VAI ALLA SOLUZIONE