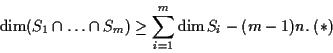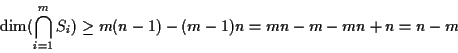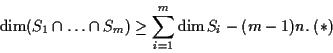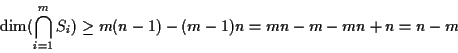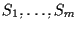
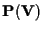
30 ESERCIZIO   Siano $S_1, \ldots ,S_m$ sottospazi proiettivi di uno spazio proiettivo $\mathbf{P(V)}$ di dimensione $n.$
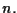
Provare che vale la relazione

\begin{displaymath}\dim (S_1 \cap \ldots \cap S_m) \geq \sum _{i=1}^{m} \dim S_i -(m-1)n.\; (\ast )\end{displaymath}

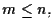
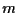
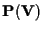
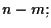
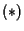
In particolare, quindi, dato $m \leq n,$ $m$ iperpiani di $\mathbf{P(V)}$ hanno in comune un sottospazio proiettivo la cui dimensione è almeno $n-m;$ infatti, in questo caso, la relazione $(\ast)$ si scrive

\begin{displaymath}\dim (\bigcap _{i=1} ^{m} S_i) \geq m(n-1)-(m-1)n=mn-m-mn+n=n-m\end{displaymath}

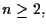
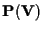
(per esempio: se $n \geq 2,$ due iperpiani di $\mathbf{P(V)}$ hanno almeno un punto in comune).

VAI ALLA SOLUZIONE