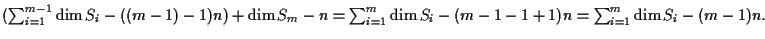Soluzione
Proviamo tale disuguaglianza per induzione su 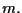
Per 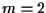 la disuguaglianza è soddisfatta, infatti (corollario 25)
la disuguaglianza è soddisfatta, infatti (corollario 25)
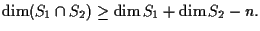
Ora proviamo che, supponendo che la relazione 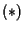 sia vera per
sia vera per 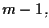 allora
allora
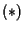 vale anche per
vale anche per 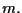 Infatti
Infatti
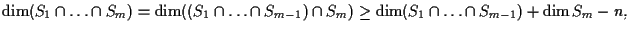 e per l'ipotesi induttiva il secondo membro
di tale disuguaglianza è maggiore o uguale di
e per l'ipotesi induttiva il secondo membro
di tale disuguaglianza è maggiore o uguale di