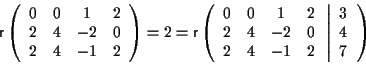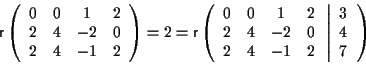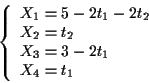11.2 La risposta alla prima domanda è affermativa, infatti il sistema è compatibile come si vede utilizzando il teorema di Rouché-Capelli:

\begin{displaymath}\mathsf{r} \left(\begin{array}{cccc} 0 & 0 & 1 & 2 \\ 2 & ... ...left\vert\begin{array}{c}3\\ 4\\ 7\end{array}\right.\right)\end{displaymath}

Per ottenere questo risultato si può ottenere tramite un'eliminazione di Gauss sulla matrice orlata o più semplicemente "ad occhio" osservando che la prima riga della matrice orlata è uguale alla differenza tra la terza e la seconda (e queste ultime due non sono proporzionali).
A questo punto possiamo possiamo dire che il sottospazio rappresentato rispetto a 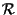$\mathcal{R}$ dalle equazioni precedenti è un piano affine di 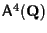$\mathsf{A}^{4}(\mathbf{Q})$ e per trovare equazioni parametriche (vedi proposizione 10) sarà sufficiente risolvere il sistema: con qualche passaggio si trova, ad esempio,

\begin{displaymath}\left\{\begin{array}{l} X_1= 5-2t_1-2t_2 \\ X_2= t_2\\ X_3= 3-2t_1\\ X_4= t_1 \end{array} \end{displaymath}

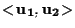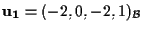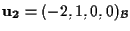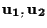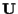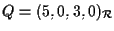Di qui otteniamo che abbiamo a che fare con il sottospazio di giacitura $<\! \mathbf{u_1},\mathbf{u_2}\!>$ ove $\mathbf{u_1}=(-2,0,-2,1)_{\mathcal{B}}$ e $\mathbf{u_2}=(-2,1,0,0)_{\mathcal{B}}$ (e in effetti $\mathbf{u_1},\mathbf{u_2}$ costituiscono una base per $\mathbf{U}$) e passante per il punto $Q=(5,0,3,0)_{\mathcal{R}}$.

torna alla teoria