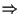)
È vera in generale (vedi primo punto di proposizione 12).
)
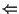Se
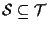allora
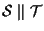in generale; supponiamo che
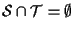e facciamo vedere che
;
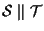equivalentemente dimostreremo l'implicazione
;
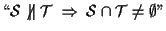certamente da
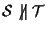segue
;
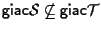da ciò segue, da considerazioni di algebra lineare, che
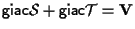e di qui, procedendo esattamente come nella dimostrazione dell'esercizio 16.1 della sezione "Sottospazi affini" si trova che
.
|
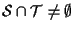