La retta>>Equazioni parametriche >>Teorema 2.2>>dimostrazione

Dimostrazione 2.2

Data nello spazio V03 una retta r, fissiamo arbitrariamente su di essa due punti distinti P1, P2 di coordinate :

P1= (x1, y1, z1)
,
P2 = (x2, y2, z2)
 
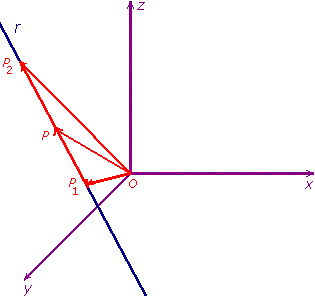
e    un punto P = (x, y, z) generico dello spazio.
 
Consideriamo allora i vettori equipollenti rispettivamente ai vettori ,, che sono dati per la regola della differenza tra vettori da:
 
= -
;
= -
 

Si ha che:
 
P r
= + t( - )
   

che equivale a dire, usando le coordinate dei punti:
   
x = x1 + t(x2 - x1)
P = (x, y, z) r
y = y1 + t(y2 - y1)
   
z = z1 + t(z2 - z1)

da cui la tesi, ponendo :

l = x2 - x1
m = y2 - y1
n = z2 - z1
 

Ovviamente se l'origine degli assi, O, appartiene alla retta, l'equazione parametrica si semplifica;

prendendo P1 = (0, 0, 0) diventa:

   
x = lt
P = (x, y, z) r
y = mt
   
z = nt


Viceversa data una terna di equazioni del tipo:

x = x1 + lt
y = y1 + mt
z = z1 + nt

si verifica che queste sono le equazioni parametriche della retta P1P2 , con P1= (x1, y1, z1) e

P2= (x1 + l, y1 + m, z1 + n), e il teorema è dimostrato.

 
torna al teorema