Dato un piano π in un sistema di riferimento cartesiano ortogonale fissiamo un punto P= (x0, y0, z0) 
π e consideriamo un generico punto Q = (x, y, z) nello spazio. Vogliamo vedere quali condizioni imporre alle coordinate (x, y, z) per avere che Q stia su π .
Prendiamo un vettore 
= (A, B,C), perpendicolare al piano π.
Poiché PQ ^ allora, per una proprietà del prodotto scalare, avremo:
  = ||||cos(π/2)= 0 |
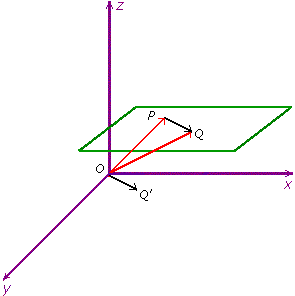
Consideriamo allora il vettore 
parallelo e di uguale modulo a .
Per la regola della differenza tra vettori avremo che:
=  -  = (x - x0, y - y0, z - z0) |
e quindi:
= 0  = 0 |
(x - x0, y - y0, z - z0)(A, B, C) = 0 |
Da cui :
| A(x - x0) + B(y - y0) + C( z - z0) = 0 |
Concludendo, posto D = - Ax0 - By0 - Cz0, otterremo che le condizioni perché Q stia sul piano sono date proprio dall'equazione (detta equazione cartesiana del piano):
Ax + By + Cz + D = 0.
La dimostrazione può anche essere visualizzata con la seguente animazione che mostra come, dati un
punto
P = (x0, y0, z0) ed un vettore fissato w = (a, b, c), arrivare all'equazione cartesiana ax + by + cz + d = 0 del piano passante per P e perpendicolare a w.
P = (x0, y0, z0) ed un vettore fissato w = (a, b, c), arrivare all'equazione cartesiana ax + by + cz + d = 0 del piano passante per P e perpendicolare a w.
 |
Torna al teorema |