

- 1.
- Data la base canonica
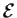 su
su
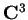 e la forma hermitiana
e la forma hermitiana 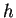 definita da
definita da
vogliamo calcolare il sottospazio ortogonale a
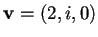 .
.
Determiniamo le soluzioni del sistema omogeneo:
equivalente all'equazione:
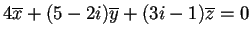
.
Quindi lo spazio cercato è:
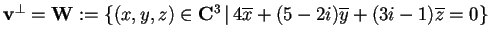
.
Tale sottospazio ortogonale si potrà meglio scrivere come:
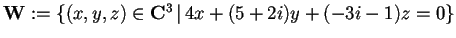
.
- 2.
- Sia
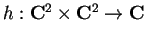 una forma hermitiana definita da
una forma hermitiana definita da
ove
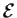 è la base canonica; allora per trovare una base diagonalizzante si procede in modo analogo al caso reale, quindi
prendiamo un vettore non isotropo, ad esempio,
è la base canonica; allora per trovare una base diagonalizzante si procede in modo analogo al caso reale, quindi
prendiamo un vettore non isotropo, ad esempio,
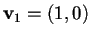 e calcoliamo:
e calcoliamo:
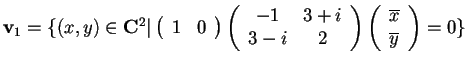 .
.
L'equazione che risolve il sistema è:
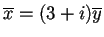 ,
quindi
,
quindi
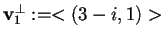
;
allora una base diagonalizzante per 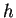 è
è
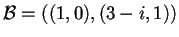 ,
infatti si ottiene
,
infatti si ottiene




su
e la forma hermitiana
definita da
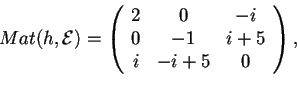
.
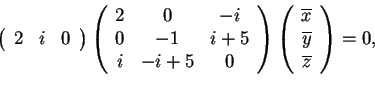
.
Tale sottospazio ortogonale si potrà meglio scrivere come:.
.
una forma hermitiana definita da
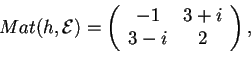
è la base canonica; allora per trovare una base diagonalizzante si procede in modo analogo al caso reale, quindi prendiamo un vettore non isotropo, ad esempio,
e calcoliamo:
.
, quindi
allora una base diagonalizzante per;
è
, infatti si ottiene
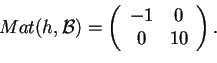


 Teoria
Teoria