
 Data la forma hermitiana
Data la forma hermitiana
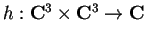 tale che rispetto alla base canonica risulta
tale che rispetto alla base canonica risulta
- a)
- Determinare un vettore
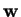 perpendicolare a
perpendicolare a
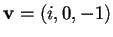 .
.
- b)
- Trovare una base diagonalizzante per
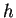 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
-
- Prendiamo come primo vettore non isotropo della base diagonalizzante
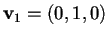 poiché
poiché
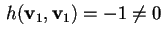 ,
allora risolviamo il sistema
,
allora risolviamo il sistema
da cui otteniamo l'equazione
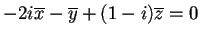 ;
quindi
;
quindi
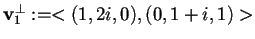
.
Ora poniamo
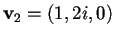 ,
quindi calcoliamo il sottospazio ortogonale relativo al secondo vettore:
,
quindi calcoliamo il sottospazio ortogonale relativo al secondo vettore:
che è equivalente all'equazione
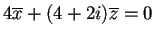 .
.
L'intersezione dei due sottospazi ortogonali fornisce le coordinate del terzo vettore della base, cioè se risolviamo il sistema
una soluzione è
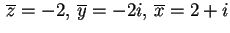 ;
quindi
;
quindi
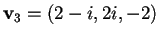 .
.
Una base diagonalizzante per 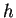 sarà
sarà
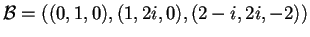 ;
infatti svolgendo i calcoli si trova che
;
infatti svolgendo i calcoli si trova che



Data la forma hermitiana
tale che rispetto alla base canonica risulta
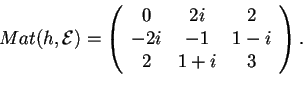
perpendicolare a
.
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
e scegliere un vettore che appartenga a questo sottospazio:
.
,
otteniamo un vettore
tale che
.
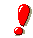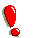
poiché
, allora risolviamo il sistema
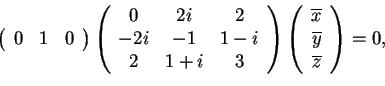
; quindi
Ora poniamo.
, quindi calcoliamo il sottospazio ortogonale relativo al secondo vettore:
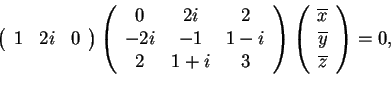
.
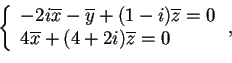
; quindi
.
sarà
; infatti svolgendo i calcoli si trova che
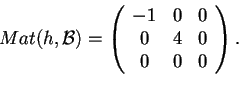


 Teoria
Teoria