

- 2.
- Data la matrice
- a)
- calcolare per quali valori di
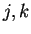 la matrice è hermitiana.
la matrice è hermitiana.
- b)
- Dopo aver sostituito i valori trovati in a) e posto
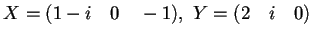 ,
dimostrare che,
,
dimostrare che,
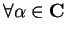 ,
vale
,
vale
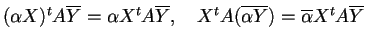
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- Punto a)
- Sappiamo che, affinché
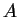 sia hermitiana, gli elementi sulla diagonale principale devono essere reali, mentre gli elementi
sia hermitiana, gli elementi sulla diagonale principale devono essere reali, mentre gli elementi 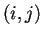 devono essere i coniugati di quelli
devono essere i coniugati di quelli 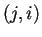 ,
quindi poniamo
,
quindi poniamo
Punto
b)
- b)
- Sostituendo i valori trovati, otteniamo la matrice
quindi, per
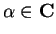 ,
abbiamo che:
,
abbiamo che:
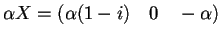
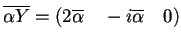
allora
allora
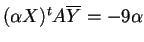 ,
mentre
,
mentre
da cui
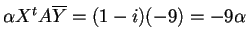 .
.
allora
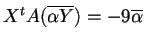 ,
infatti
,
infatti
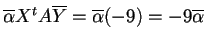 .
.





la matrice è hermitiana.
, dimostrare che,
, vale
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzionesia hermitiana, gli elementi sulla diagonale principale devono essere reali, mentre gli elementi
devono essere i coniugati di quelli
, quindi poniamo
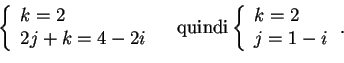
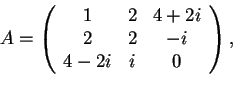
, abbiamo che:
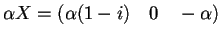
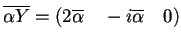
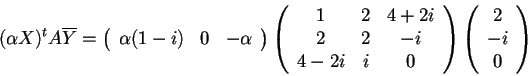
, mentre
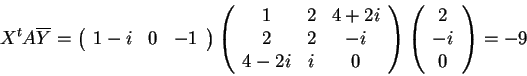
.
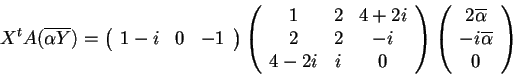
, infatti
.


 Teoria
Teoria