Esercizio

Dimostrare che
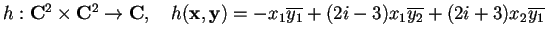
$h:\mathbf{C}^2\times\mathbf{C}^2\rightarrow\mathbf{C}, \quad h(\mathbf{x},\math... ...=-x_{1}\overline{y_{1}}+(2i-3)x_{1}\overline{y_{2}}+(2i+3)x_{2}\overline{y_{1}}$
è una forma hermitiana, mentre
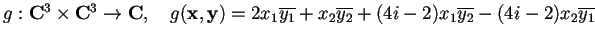
$g:\mathbf{C}^3\times\mathbf{C}^3\rightarrow\mathbf{C}, \quad g(\mathbf{x},\math... ...}+x_{2}\overline{y_{2}}+(4i-2)x_{1}\overline{y_{2}}-(4i-2)x_{2}\overline{y_{1}}$
non lo è. Vuoi un aiuto?
Per vedere la soluzione totale, clicca , oppure clicca per visualizzare ogni singolo passo della soluzione.
I passo:
Verifichiamo che $h$ soddisfa le quattro condizioni necessarie per essere una forma hermitiana:
1.
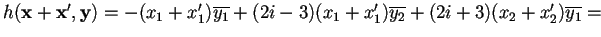
$h(\mathbf{x}+\mathbf{x}',\mathbf{y})=-(x_{1}+x'_{1})\overline{y_{1}}+(2i-3)(x_{1}+x'_{1})\overline{y_{2}}+(2i+3)(x_{2}+x'_{2})\overline{y_{1}}=$
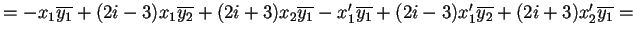
$=-x_{1}\overline{y_{1}}+(2i-3)x_{1}\overline{y_{2}}+(2i+3)x_{2}\overline{y_{1}}-x'_{1}\overline{y_{1}}+(2i-3)x'_{1}\overline{y_{2}}+(2i+3)x'_{2}\overline{y_{1}}=$
$=h(\mathbf{x},\mathbf{y})+h(\mathbf{x}',\mathbf{y})$.
2.
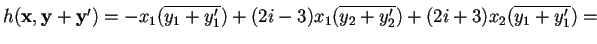
$h(\mathbf{x},\mathbf{y}+\mathbf{y}')=-x_{1}(\overline{y_{1}+y'_{1}})+(2i-3)x_{1}(\overline{y_{2}+y'_{2}})+(2i+3)x_{2}(\overline{y_{1}+y'_{1}})=$
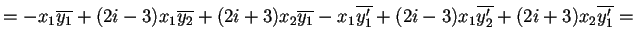
$=-x_{1}\overline{y_{1}}+(2i-3)x_{1}\overline{y_{2}}+(2i+3)x_{2}\overline{y_{1}}-x_{1}\overline{y'_{1}}+(2i-3)x_{1}\overline{y'_{2}}+(2i+3)x_{2}\overline{y'_{1}}=$
$=h(\mathbf{x},\mathbf{y})+h(\mathbf{x},\mathbf{y}')$.
3.
Sia $\alpha \in \mathbf{C}$, allora
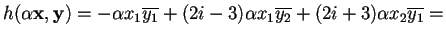
$h(\alpha\mathbf{x},\mathbf{y})= -\alpha x_{1}\overline{y_{1}}+(2i-3)\alpha x_{1}\overline{y_{2}}+(2i+3)\alpha x_{2}\overline{y_{1}}=$
$=\alpha (-x_{1}\overline{y_{1}}+(2i-3)x_{1}\overline{y_{2}}+(2i+3)x_{2}\overline{y_{1}})=\alpha h(\mathbf{x},\mathbf{y})$.
4.
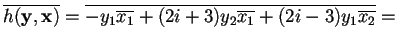
$\overline{h(\mathbf{y},\mathbf{x})}=\overline{-y_{1}\overline{x_{1}}+(2i+3)y_{2}\overline{x_{1}}+(2i-3)y_{1}\overline{x_{2}}}=$
$=-x_{1}\overline{y_{1}}+(2i-3)x_{1}\overline{y_{2}}+(2i+3)x_{2}\overline{y_{1}}=h(\mathbf{x},\mathbf{y})$.
II passo:  

L'applicazione $g$ non è una forma hermitiana perché non è verificata la condizione

$g(\mathbf{x},\mathbf{y})=\overline{g(\mathbf{y},\mathbf{x})}$,
infatti

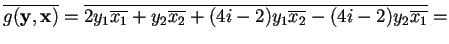
$\overline{g(\mathbf{y},\mathbf{x})}=\overline{2y_{1}\overline{x_{1}}+y_{2}\overline{x_{2}}+(4i-2)y_{1}\overline{x_{2}}-(4i-2)y_{2}\overline{x_{1}}}=$
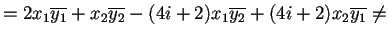
$=2x_{1}\overline{y_{1}}+x_{2}\overline{y_{2}}-(4i+2)x_{1}\overline{y_{2}}+(4i+2)x_{2}\overline{y_{1}}\neq$
$\neq 2x_{1}\overline{y_{1}}+x_{2}\overline{y_{2}}+(4i-2)x_{1}\overline{y_{2}}-(4i-2)x_{2}\overline{y_{1}}=g(\mathbf{x},\mathbf{y})$.