Esercizi

1.
Costruire un endomorfismo unitario che abbia come autovalori $\lambda=3$, con molteplicità 2, e $\mu=-2$, con molteplicità 1, e per il quale una base ortonormale non sia quella canonica.

Vuoi un aiuto?
Per vedere la soluzione, clicca

Soluzione
Prendiamo una base ortonormale $\mathcal{B}=\frac{1}{\sqrt{2}}(i,0,1),\frac{1}{\sqrt{2}}(0,1+i,0),\frac{1}{\sqrt{2}}(-i,0,1))$, allora poniamo

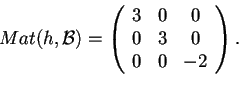
\begin{displaymath}Mat(h,\mathcal{B})=\begin{array}({ccc}) 3 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & -2 \end{array}. \end{displaymath}

Per calcolare l'endomorfismo richiesto, basta determinare il nuovo endomorfismo associato alla matrice $M_{\mathcal{E}}(h)$ che si ottiene calcolando
$(M_{\mathcal{B,E}}(h))^{t}Mat(h,\mathcal{B})\overline{M_{\mathcal{B,E}}(h)}$,
cioè:

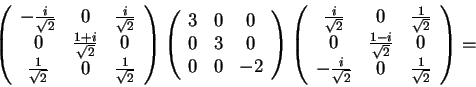
\begin{displaymath}\begin{array}({ccc}) -\frac{i}{\sqrt{2}} & 0 & \frac{i}{\sqr... ... -\frac{i}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}= \end{displaymath}


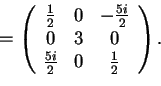
\begin{displaymath}=\begin{array}({ccc}) \frac{1}{2} & 0 & -\frac{5i}{2}\\ 0 & 3 & 0\\ \frac{5i}{2} & 0 & \frac{1}{2} \end{array}. \end{displaymath}

Allora un endomorfismo che soddisfa le richieste è
$h(x,y,z)=\frac{1}{2}(x+5iz,3y,-5ix+z)$.