Esempio

Si consideri il prodotto hermitiano standard e l'operatore $f:\mathbf{C}^3\rightarrow\mathbf{C}^3$ tale che
$f(x,y,z)=(x-2iy,2ix+z,y+2z)$.
Allora $f$ è hermitiano; infatti, presi $\mathbf{v}=(x,y,z),\mathbf{w}=(x',y',z')$, si ha:
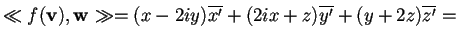
$\ll f(\mathbf{v}),\mathbf{w} \gg = (x-2iy)\overline{x'}+(2ix+z)\overline{y'}+(y+2z)\overline{z'}=$
$=x(\overline{x'}+2i\overline{y'})+y(-2i\overline{x'}+\overline{z'})+z(\overline{y'}+2\overline{z'})=\ll \mathbf{v},f(\mathbf{w})\gg$.
Poniamo $A=M_{\mathcal{E}}(f)$, che è la matrice associata di $f$ rispetto alla base canonica, allora gli autovalori di $f$ sono dati da

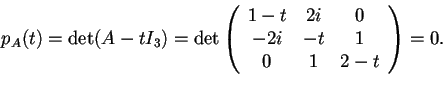
\begin{displaymath}p_{A}(t)=\det(A-tI_{3})=\det \begin{array}({ccc}) 1-t & 2i & 0\\ -2i & -t & 1\\ 0 & 1 & 2-t \end{array}=0. \end{displaymath}

Risolvendo, abbiamo una equazione di terzo grado: $-t^3+3t^2+3t-9=0$, le sui soluzioni $t=3, t=\pm \sqrt{3}$, danno tre autovalori distinti che, come prevedibile, sono reali.