Esercizi

2.
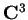Dato l'endomorfismo unitario $h$ su $\mathbf{C}^3$
$h(x,y,z)=(-2x,\sqrt{2}z,\sqrt{2}y-z)$,
trovare una base ortonormale di autovettori per $h$.

Vuoi un aiuto?
Per vedere la soluzione, clicca

Soluzione
Calcoliamo il polinomio caratteristico della matrice associata:

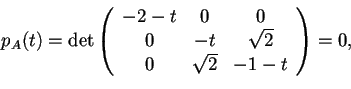
\begin{displaymath}p_{A}(t)=\det \begin{array}({ccc}) -2-t & 0 & 0\\ 0 & -t & \sqrt{2}\\ 0 & \sqrt{2}& -1-t \end{array}=0, \end{displaymath}

da cui otteniamo l'equazione $(t+2)^2(t-1)=0$.
Quindi gli autovalori sono: $t=1, t=-2$ (con molteplicità 2). Calcoliamo l'autospazio relativo a $t=2$:
$\mathbf{H}_{-2}=ker(f+2id)$ è lo spazio delle soluzioni del sistema omogeneo:

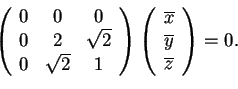
\begin{displaymath}\begin{array}({ccc}) 0 & 0 & 0 \\ 0 & 2 & \sqrt{2}\\ 0 &... ...overline{x}\\ \overline{y}\\ \overline{z} \end{array}=0. \end{displaymath}

Svolgendo i calcoli, ricaviamo che $\mathbf{H}_{-2}=<(1,0,0),(0,1,-\sqrt{2})>$; quindi i primi due vettori della base ortonormale saranno $\mathbf{v}_{1}=(1,0,0), \, \mathbf{v}_{2}=\frac{1}{\sqrt{3}}(0,1,-\sqrt{2})>$.
Procediamo analogamente per l'altro autovalore $t=1$:
$\mathbf{H}_{1}=ker(f-id)$ è lo spazio delle soluzioni del sistema omogeneo:

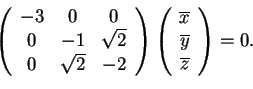
\begin{displaymath}\begin{array}({ccc}) -3 & 0 & 0 \\ 0 & -1 & \sqrt{2}\\ 0... ...overline{x}\\ \overline{y}\\ \overline{z} \end{array}=0. \end{displaymath}

Quindi, otteniamo che $\mathbf{H}_{1}=<(0,\sqrt{2},1)>$. Perciò il terzo vettore sarà $\mathbf{v}_{3}=\frac{1}{\sqrt{3}}(0,-\sqrt{2},1)$.
Abbiamo trovato allora che una base ortonormale di autovettori per $h$ è:
$\mathcal{C}=((1,0,0),\frac{1}{\sqrt{3}}(0,1,-\sqrt{2}),\frac{1}{\sqrt{3}}(0,-\sqrt{2},1)))$.