

- 2.
- Si consideri la base canonica e l'endomorfismo
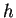 su
su
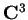 tale che:
tale che:
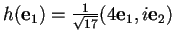
,
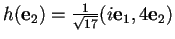
.
- a)
- Stabilire se
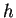 è unitario verificando se la matrice associata appartiene al gruppo unitario di ordine 2.
è unitario verificando se la matrice associata appartiene al gruppo unitario di ordine 2.
- b)
- Trovare gli autovalori di
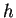 .
.
- c)
- Siano
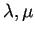 autovalori di
autovalori di 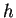 ;
è possibile che la proiezione del vettore che genera l'autospazio relativo a
;
è possibile che la proiezione del vettore che genera l'autospazio relativo a 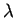 sull'autospazio relativo a
sull'autospazio relativo a 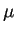 sia di norma 1? Perché?
sia di norma 1? Perché?
- d)
- Trovare due basi ortonormali per
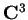 rispetto al prodotto hermitiano standard.
rispetto al prodotto hermitiano standard.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- Punto a)
- Prendiamo una base ortonormale; per semplicità scegliamo quella canonica. Allora abbiamo
tale che
Quindi, poiché la matrice associata di 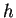 è unitaria rispetto ad una base ortonormale,
è unitaria rispetto ad una base ortonormale, 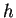 è un endomorfismo unitario.
è un endomorfismo unitario.
Punto
b)
-
- Grazie alle proprietà degli endomorfismi unitari, per calcolare una nuova base ortonormale, basta prenderne una, ad esempio quella canonica, e calcolare
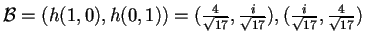 .
.




su
tale che:
,
.
è unitario verificando se la matrice associata appartiene al gruppo unitario di ordine 2.
.
autovalori di
; è possibile che la proiezione del vettore che genera l'autospazio relativo a
sull'autospazio relativo a
sia di norma 1? Perché?
rispetto al prodotto hermitiano standard.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione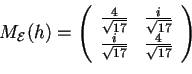
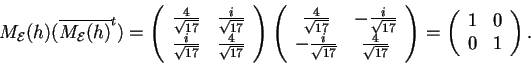
è unitaria rispetto ad una base ortonormale,
è un endomorfismo unitario.
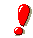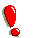
, si ha:
,
, che sono rispettivamente gli autovalori
.
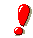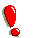
di
è perpendicolare a
, perciò si ha
.
.


 Teoria
Teoria