Esercizi

2.
Per quali valori di $k\in\mathbf{C}$ la base $\mathcal{C}=((0,k,0),\frac{1}{\sqrt{2}}(0,0,1),\frac{1}{\sqrt{2}}(1+i,-2k,i-1))$ è ortonormale per il prodotto hermitiano $h$ tale che

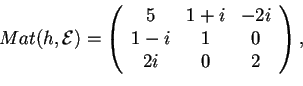
\begin{displaymath}Mat(h,\mathcal{E})= \begin{array}({ccc}) 5 & 1+i & -2i\\ 1-i & 1 & 0\\ 2i & 0 & 2 \end{array}, \end{displaymath}

ove $\mathcal{E}$ è la base canonica?

Vuoi un aiuto?
Per vedere la soluzione, clicca

Soluzione
Sappiamo che una base per $h$ è ortonormale se rispetto a tale base la matrice associata di $h$ è la matrice identità; quindi, posto $k=a+ib, \,$ con $a,b \in \mathbf{R}$, abbiamo che
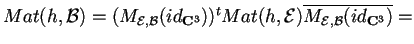
$Mat(h,\mathcal{B})=(M_{\mathcal{E,B}}(id_{\mathbf{C}^3}))^{t}Mat(h,\mathcal{E})\overline{M_{\mathcal{E,B}}(id_{\mathbf{C}^3})}=$

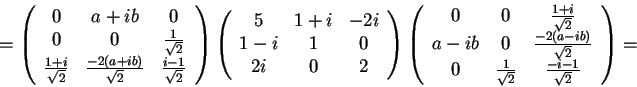
\begin{displaymath}=\begin{array}({ccc}) 0 & a+ib & 0\\ 0 & 0 & \frac{1}{\sqr... ... 0 & \frac{1}{\sqrt{2}} & \frac{-i-1}{\sqrt{2}} \end{array}= \end{displaymath}


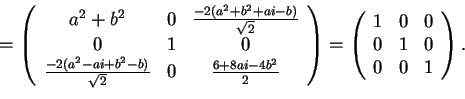
\begin{displaymath}=\begin{array}({ccc}) a^2+b^2 & 0 & \frac{-2(a^2+b^2+ai-b)}{... ...}({ccc}) 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}. \end{displaymath}

Allora poniamo:

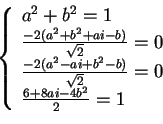
\begin{displaymath}\left \{ \begin{array}{l} a^2+b^2=1\\ \frac{-2(a^2+b^2+ai-... ...)}{\sqrt{2}}=0\\ \frac{6+8ai-4b^2}{2}=1 \end{array}\right. \end{displaymath}

e risolvendo il sistema otteniamo $a=0, b=1$, quindi $k=i$.