
 Dati i due endomorfismi
Dati i due endomorfismi
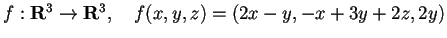 ;
;
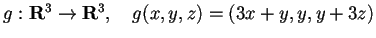 .
.
- a)
- Dimostrare che
 è autoaggiunto.
è autoaggiunto.
- b)
- Costruire l'endomorfismo
 aggiunto di
aggiunto di  e verificare che, presi
e verificare che, presi
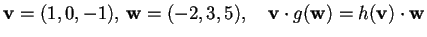 .
.
- c)
- Verificare che
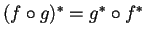 e
e
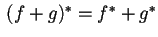 .
.
- d)
- È vero che
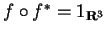 ?
?
- e)
- Se prendiamo la base
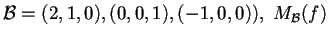 è simmetrica? Perché?
è simmetrica? Perché?
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
- Punto a)
- L'endomorfismo
 è autoaggiunto se
è autoaggiunto se 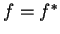 ,
quindi se, rispetto ad una base ortonormale, la matrice associata è simmetrica.
,
quindi se, rispetto ad una base ortonormale, la matrice associata è simmetrica.
Prendiamo la base canonica, allora
è simmetrica, quindi  è autoaggiunto.
è autoaggiunto.
Punto
b) 
- I passo:
- La matrice associata di
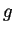 rispetto alla base canonica è:
rispetto alla base canonica è:
quindi
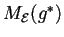 sarà uguale alla sua trasposta:
sarà uguale alla sua trasposta:
e l'endomorfismo 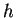 sarà definito da:
sarà definito da:
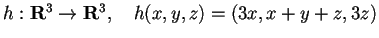
.
II passo:

-
- La matrice risultante non è simmetrica perché la base
 non è ortonormale.
non è ortonormale.



Dati i due endomorfismi
;
.
è autoaggiunto.
aggiunto di
e verificare che, presi
.
e
.
?
è simmetrica? Perché?
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
è autoaggiunto se
, quindi se, rispetto ad una base ortonormale, la matrice associata è simmetrica.
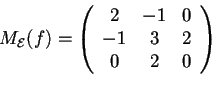
è autoaggiunto.

rispetto alla base canonica è:
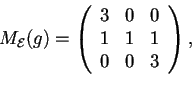
sarà uguale alla sua trasposta:
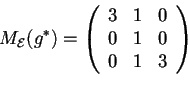
sarà definito da:
.

non è ortonormale.


 Teoria
Teoria