Esempi

1.
Consideriamo la seguente applicazione $f \in End(\mathbf{R}^2)$:
$f:\mathbf{R}^2 \rightarrow \mathbf{R}^2, \qquad f(x,y):= (x+y,2x-y)$.
La matrice associata a $f$ è:

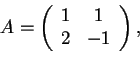
\begin{displaymath}A= \begin{array}({cc}) 1 & 1\\ 2 & -1 \end{array}, \end{displaymath}

Ora proviamo a fare la trasposta della matrice A:

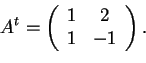
\begin{displaymath}A^{t}= \begin{array}({cc}) 1 & 2\\ 1 & -1 \end{array}. \end{displaymath}

che determinerà l'endomorfismo $g(x,y)=(x+2y,x-y)$. Verifichiamo che $g$ è l'endomorfismo aggiunto di $f$:
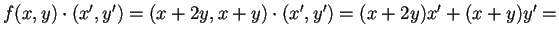
$f(x,y) \cdot (x',y')=(x+2y,x+y) \cdot (x',y')= (x+2y)x'+(x+y)y'=$
$=(x'+2y')x+(x'-y')y=(x,y) \cdot g(x',y')$;
quindi $g=f^{*}$.

2.
Consideriamo ora il seguente endomorfismo:
$f:\mathbf{R}^2 \rightarrow \mathbf{R}^2, \qquad f(x,y):= (2x+y,x-2y)$.
La matrice associata a $f$ rispetto alla base canonica $\mathcal{E}$ è:

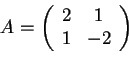
\begin{displaymath}A= \begin{array}({cc}) 2 & 1\\ 1 & -2 \end{array} \end{displaymath}

e, poiché $A$ è simmetrica e $\mathcal{E}$ è ortonormale, $f$ sarà autoaggiunto.
Se invece prendiamo una base $\mathcal{C}=((1,1),(0,1))$, non ortonormale, la matrice associata non sarà più simmetrica, infatti:

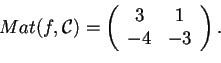
\begin{displaymath}Mat(f,\mathcal{C})= \begin{array}({cc}) 3 & 1\\ -4 & -3 \end{array}. \end{displaymath}