

- 2.
- Si consideri lo spazio euclideo
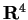 con il prodotto scalare standard e sia
con il prodotto scalare standard e sia
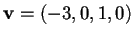 .
Allora
.
Allora
- a)
- il vettore
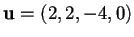 è perpendicolare a
è perpendicolare a
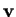 ?
?
- b)
- in caso di risposta negativa, calcolare l'angolo compreso fra i due vettori.
- c)
- calcolare per quali valori di
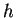 il vettore
il vettore
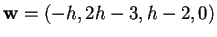 è parallelo a
è parallelo a
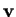 ? per quali forma con il vettore un angolo di 45 gradi?
? per quali forma con il vettore un angolo di 45 gradi?
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- Punto a)
- I due vettori sono perpendicolari se formano un angolo
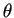 di 90 gradi, cioè se
di 90 gradi, cioè se
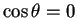 ;
ma
;
ma
quindi non sono ortogonali.
Punto
b) 
-
- L'angolo
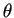 risulta:
risulta:
Punto
c)
- I passo:
- Se i due vettori sono paralleli, allora il coseno dell'angolo compreso fra le loro direzioni avrà valore +1 o -1, quindi
che, svolgendo i calcoli, per nessun valore di 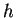 dà una identità.
dà una identità.
II passo:

In modo analogo si opera per determinare quando i due vettori formano un angolo di 45 gradi fra loro, sapendo che il coseno di tale angolo sarà
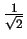 :
:
da cui, risolvendo l'equazione, si ottiene
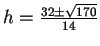 .
.




con il prodotto scalare standard e sia
. Allora
è perpendicolare a
?
il vettore
è parallelo a
? per quali forma con il vettore un angolo di 45 gradi?
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzionedi 90 gradi, cioè se
; ma
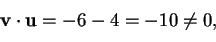

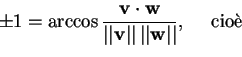
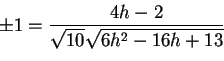
dà una identità.

:
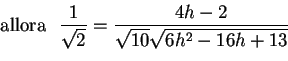
.

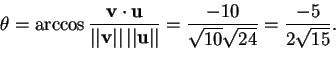

 Teoria
Teoria