
Esercizi

- 2.
- In ciascuno dei seguenti casi si dica se la seguente forma bilineare è un prodotto scalare su
, e, nei casi in cui
risulta un prodotto scalare, si determini una base ortonormale di
, sia utilizzando il procedimento di Gram-Schimdt a partire dalla base canonica, sia utilizzando il procedimento visto per determinare una base diagonalizzante per una forma bilineare simmetrica qualunque:
- a)
;
- b)
;
- c)
- sia
e sia
tale che
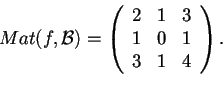
Vuoi un aiuto?
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
SoluzioneII passo:
- Punto a)
- I passo:
- Controlliamo se
è una forma definita positiva attraverso il criterio dei minori principali:
;
;
;
alloraè un prodotto scalare.
Utilizziamo prima il procedimento di ortogonalizzazione di Gram-Schimdt:
III passo:
prendiamola base canonica, allora
;
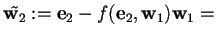
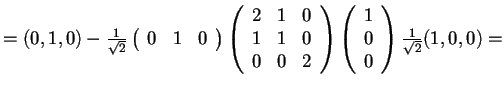
,
da cui, poiché
,
si ottiene;
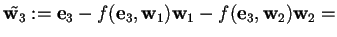
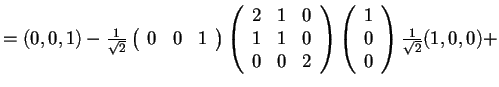
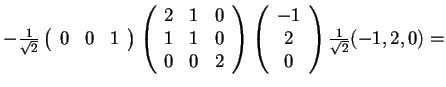
,
da cui, poiché
,
si ottiene.
La baseè la base ortonormale cercata.
Adesso procediamo attraverso la diagonalizzazione della forma bilineare simmetrica:
Punto b)
prendiamonon isotropo, infatti
, e calcoliamo il suo sottospazio ortogonale:
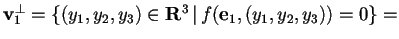
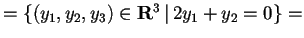
;
allora.
Scegliamo un vettore appartenente a, ad esempio
e calcoliamo il suo sottospazio ortogonale:
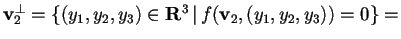
;
quindi il terzo vettore della base è dato dall'intersezione dei due sottospazi ortogonali:
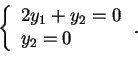
Quindi abbiamo ottenuto la base ortogonale, ove
tale che
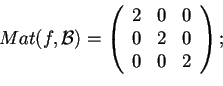
perciò la base ortonormale cercata sarà formata dai vettori:.
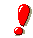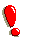
Punto c)
- Prendiamo la base canonica di
, allora
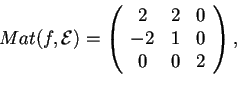
allora vediamo chenon è una forma simmetrica, quindi non può essere un prodotto scalare.
- Calcoliamo il determinante della matrice associata:
;
quindi, essendo degenere, non può essere un prodotto scalare.


 Teoria
Teoria