Esercizi

Soluzione

Sappiamo che, se indichiamo con $\mathcal{E}$ la base canonica, abbiamo che:

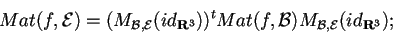
$\begin{displaymath}Mat(f,\mathcal{E})=(M_{\mathcal{B,E}}(id_{\mathbf{R}^3}))^{t}Mat(f,\mathcal{B})M_{\mathcal{B,E}}(id_{\mathbf{R}^3}); \end{displaymath}$

e, se $\mathcal{B}$ è ortogonale, $Mat(f,\mathcal{B})$ è una matrice diagonale, quindi otteniamo dalla formula sopra che:

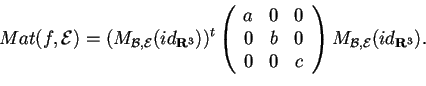
$\begin{displaymath}Mat(f,\mathcal{E})=(M_{\mathcal{B,E}}(id_{\mathbf{R}^3}))^{t}... ...0 & 0 & c \end{array} M_{\mathcal{B,E}}(id_{\mathbf{R}^3}). \end{displaymath}$

Iniziamo a calcolare la matrice di cambiamento di base:
$(1,0,0)=(1,1,0)_{\mathcal{B}}$ ,
$(0,1,0)=(2,2,1)_{\mathcal{B}}$ ,
$(0,0,1)=(0,1,0)_{\mathcal{B}}$ ,
quindi si ha:

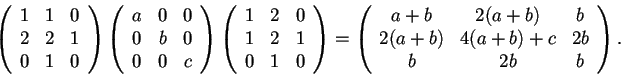
$\begin{displaymath}\begin{array}({ccc}) 1 & 1 &0\\ 2 & 2 & 1\\ 0 & 1 & 0 \... ...) & b\\ 2(a+b) & 4(a+b)+c & 2b\\ b & 2b & b \end{array}. \end{displaymath}$

Allora le forme quadratiche $q:\mathbf{R}^3 \rightarrow \mathbf{R}$ cercate sono del tipo, $\forall a,b \in \mathbf{R}$ :