

- 1.
- La base canonica è sempre ortogonale per la forma bilineare standard in ogni spazio
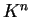 .
.
- 2.
- Prendiamo la base
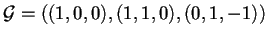 e la forma bilineare
e la forma bilineare
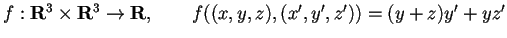
.
La base
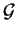 è ortogonale per
è ortogonale per 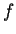 ,
perché i vettori che la formano sono ortogonali fra loro a due a due.
,
perché i vettori che la formano sono ortogonali fra loro a due a due.
- 3.
- Prendiamo
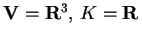 e
e 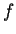 tale che
tale che
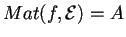 :
:
Vogliamo trovare una base diagonalizzante per 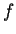 .
.
Cerco un vettore
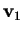 non isotropo per
non isotropo per
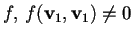 ;
;
poiché
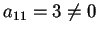 ,
si ha
,
si ha
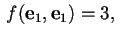 quindi
quindi
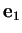 è non isotropo.
è non isotropo.
Scelgo
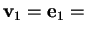 (1,0,0).
(1,0,0).
Sappiamo che
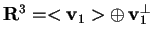
e cioè:
quindi
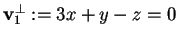 .
.
Riapplicando il precedente procedimento a
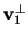 ,
consideriamo
,
consideriamo
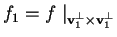 .
Avremo:
.
Avremo:
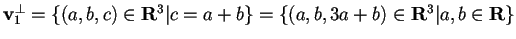 ;
;
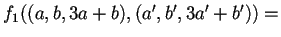 In particolare, per
In particolare, per
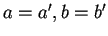 trovo
trovo
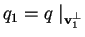 che è la forma quadratica associata a
che è la forma quadratica associata a 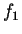 ,
cioè
,
cioè
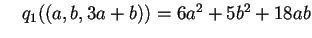 .
.
Stiamo cercando un vettore
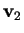 non isotropo per
non isotropo per 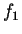 ,
cioè tale che
,
cioè tale che
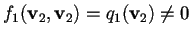
.
Per esempio prendiamo
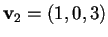 ;
infatti
;
infatti
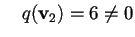 ;
;
allora
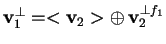 ,
con
,
con
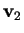 non isotropo per
non isotropo per 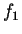 .
.
Avremo, ovviamente
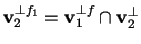 ;
e
da cui otteniamo
;
e
da cui otteniamo
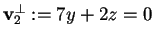 ,
e quindi:
,
e quindi:
da cui otteniamo
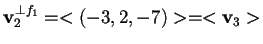 .
.
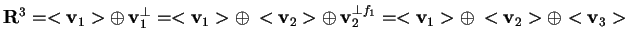
Allora
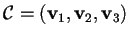 è una base diagonalizzante per
è una base diagonalizzante per
 .
.




.
e la forma bilineare
La base.
è ortogonale per
, perché i vettori che la formano sono ortogonali fra loro a due a due.
e
tale che
:
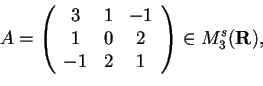
.
non isotropo per
;
, si ha
quindi
è non isotropo.
(1,0,0).
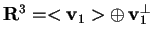
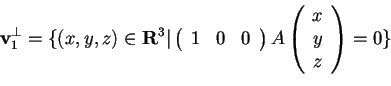
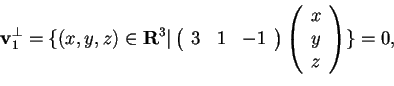
.
, consideriamo
. Avremo:
;
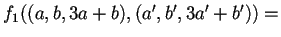 In particolare, per
In particolare, per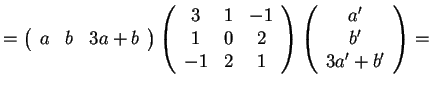
trovo
che è la forma quadratica associata a
, cioè
.
non isotropo per
, cioè tale che
Per esempio prendiamo.
; infatti
;
, con
non isotropo per
.
; e
da cui otteniamo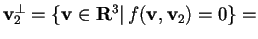
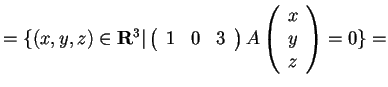
, e quindi:
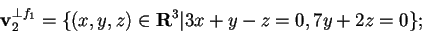
.
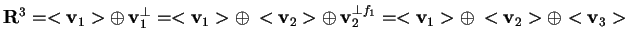
è una base diagonalizzante per
.

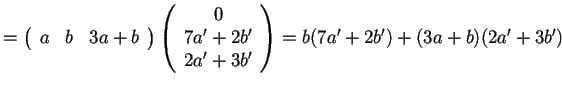
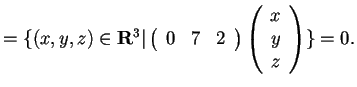

 Teoria
Teoria