

- 2.
- Si consideri
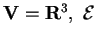 la base canonica e
la base canonica e
Sia
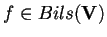 tale che
tale che
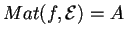 .
Si dica se
.
Si dica se 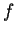 ha una base ortogonale, e, in caso di risposta affermativa, si determini una matrice diagonale congruente ad
ha una base ortogonale, e, in caso di risposta affermativa, si determini una matrice diagonale congruente ad 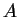 .
.
Vuoi un aiuto?
Per vedere la soluzione, clicca  .
.
Soluzione
-
- Esiste certamente una base diagonale per
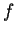 ,
iniziamo a cercarla:
prendiamo un vettore
,
iniziamo a cercarla:
prendiamo un vettore
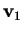 non isotropo per
non isotropo per
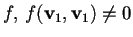
poiché
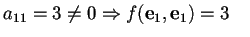 quindi
quindi
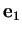 non isotropo.
non isotropo.
Scegliamo
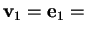 (1,0,0).
(1,0,0).
Sappiamo che
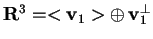
da cui otteniamo, svolgendo i calcoli, che
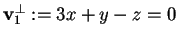 ,
quindi
,
quindi
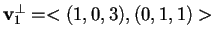 .
.
Adesso, per semplicità, scegliamo un vettore appartenente a
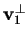 ,
ad esempio
,
ad esempio
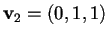 e controlliamo che non sia isotropo:
e controlliamo che non sia isotropo:
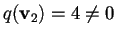 ,
quindi procediamo con il nuovo vettore.
,
quindi procediamo con il nuovo vettore.
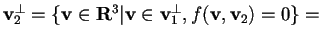
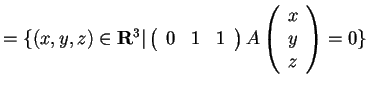
,
da cui otteniamo
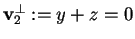 .
.
da cui otteniamo
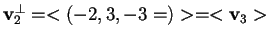 .
Allora:
.
Allora:
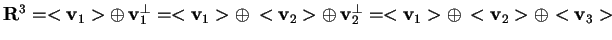 .
.
Quindi
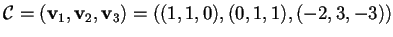 è una base diagonalizzante per
è una base diagonalizzante per 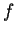 .
.
In particolare, svolgendo i calcoli, si può verificare che :
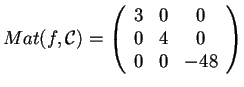
.




la base canonica e
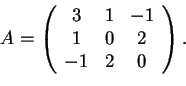
tale che
. Si dica se
ha una base ortogonale, e, in caso di risposta affermativa, si determini una matrice diagonale congruente ad
.
.
Soluzione, iniziamo a cercarla: prendiamo un vettore
non isotropo per
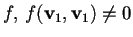
quindi
non isotropo.
(1,0,0).
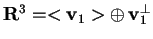
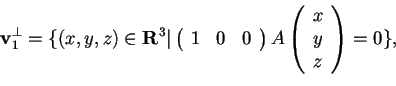
, quindi
.
, ad esempio
e controlliamo che non sia isotropo:
, quindi procediamo con il nuovo vettore.
da cui otteniamo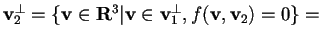
,
.
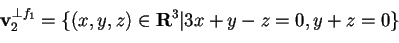
. Allora:
.
è una base diagonalizzante per
.
.


 Teoria
Teoria