

- 2.
- Si considerino le matrici
Sono 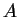 e
e 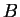 congruenti come matrici reali?
congruenti come matrici reali?
Se sì , si determini una matrice 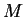 tale che
tale che 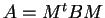 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- I passo:
- Sappiamo che, poiché le matrici diagonali definite positive, definite negative, semidefinite positive, semidefinite negative e le indefinite delle varie segnature costituiscono un insieme completo di rappresentanti per le classi di congruenza in
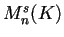 ,
due matrici saranno congruenti se apparterranno alla stessa classe, quindi se avranno la stessa segnatura.
,
due matrici saranno congruenti se apparterranno alla stessa classe, quindi se avranno la stessa segnatura.
In questo caso, sia la segnatura di 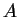 che di
che di  è (2,1), quindi le due matrici sono congruenti come matrici reali
è (2,1), quindi le due matrici sono congruenti come matrici reali
(N.B. In
 ,
basta che le due matrici abbiano lo stesso rango).
,
basta che le due matrici abbiano lo stesso rango).
II passo:
Cerchiamo la matrice 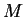 tale che
tale che 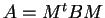 .
.
Consideriamo 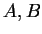 come matrici associate ad una forma bilineare simmetrica rispetto a basi diverse, in particolare poniamo:
come matrici associate ad una forma bilineare simmetrica rispetto a basi diverse, in particolare poniamo:
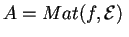 dove
dove
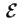 è la base canonica;
è la base canonica;
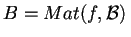 dove
dove
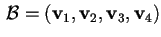 .
.
Abbiamo che:
Ora, per determinare i
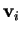 ,
basta mettere in corrispondenza i vettori rispetto ai quali
,
basta mettere in corrispondenza i vettori rispetto ai quali 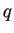 assume lo stesso segno, e poiché vogliamo
assume lo stesso segno, e poiché vogliamo
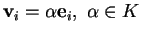 ,
avremo:
,
avremo:
-
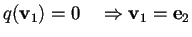 ,
infatti se
,
infatti se
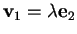 ,
,
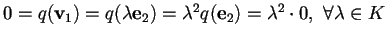 ;
;
-
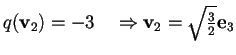 ,
infatti se
,
infatti se
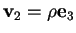 ,
,
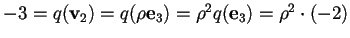 ,
allora
,
allora
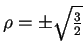 :
:
-
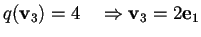 ,
infatti se
,
infatti se
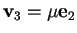 ,
,
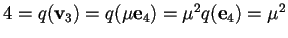 ,
allora
,
allora 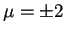 ;
;
-
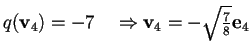 ,
infatti se
,
infatti se
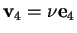 ,
,
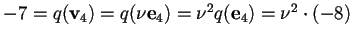 ,
allora
,
allora
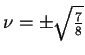 .
.
La base sarà quindi
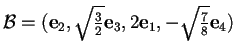 ,
,
e la matrice  sarà:
sarà:




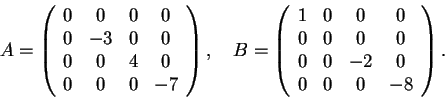
e
congruenti come matrici reali?
tale che
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione, due matrici saranno congruenti se apparterranno alla stessa classe, quindi se avranno la stessa segnatura.
che di
è (2,1), quindi le due matrici sono congruenti come matrici reali
, basta che le due matrici abbiano lo stesso rango).
tale che
.
come matrici associate ad una forma bilineare simmetrica rispetto a basi diverse, in particolare poniamo:
dove
è la base canonica;
dove
.
, basta mettere in corrispondenza i vettori rispetto ai quali
assume lo stesso segno, e poiché vogliamo
, avremo:
, infatti se
,
;
, infatti se
,
, allora
:
, infatti se
,
, allora
;
, infatti se
,
, allora
.
,
sarà:
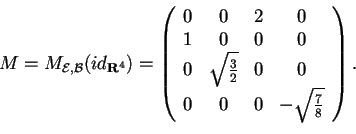


 Teoria
Teoria