

- 1.
- Posto
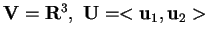 ,
ove
,
ove
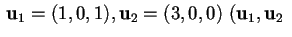 sono linearmente indipendenti) e data la matrice non degenere
sono linearmente indipendenti) e data la matrice non degenere
vogliamo calcolare
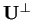 .
.
Iniziamo a calcolare
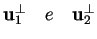 .
.
da cui otteniamo:
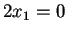
;
da cui otteniamo
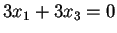
.
Dalla loro intersezione ricaviamo
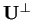 ,
che sarà definito da:
,
che sarà definito da:
Si ha che
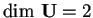 poiché la sua base è formata da 2 vettori linearmente indipendenti, mentre per
poiché la sua base è formata da 2 vettori linearmente indipendenti, mentre per
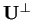 sappiamo che due equazioni cartesiane indipendenti in
sappiamo che due equazioni cartesiane indipendenti in
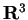 individuano un sottospazio di dimensione 1; tale dimensione è quella aspettata, poiché:
individuano un sottospazio di dimensione 1; tale dimensione è quella aspettata, poiché:
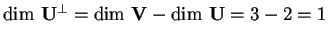
.
- 2.
- Prendiamo su
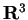 la forma bilineare simmetrica
la forma bilineare simmetrica 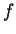 associata alla matrice:
associata alla matrice:
Vogliamo determinare
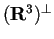 .
.
Lo spazio dei vettori ortogonali a
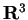 rispetto a
rispetto a 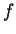 è lo spazio delle soluzioni del sistema omogeneo la cui matrice dei coefficienti è la stessa
è lo spazio delle soluzioni del sistema omogeneo la cui matrice dei coefficienti è la stessa 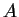 ,
che è equivalente al sistema:
,
che è equivalente al sistema:
che ci dà:
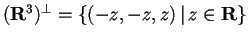
.




, ove
sono linearmente indipendenti) e data la matrice non degenere
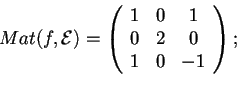
.
.
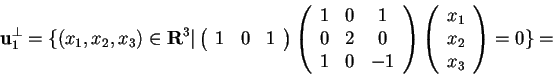
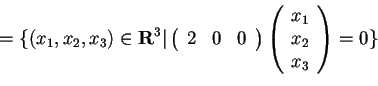
;
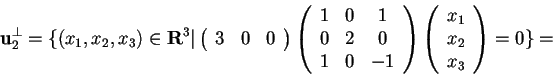
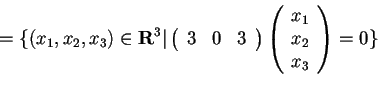
.
, che sarà definito da:
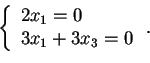
poiché la sua base è formata da 2 vettori linearmente indipendenti, mentre per
sappiamo che due equazioni cartesiane indipendenti in
individuano un sottospazio di dimensione 1; tale dimensione è quella aspettata, poiché:
.
la forma bilineare simmetrica
associata alla matrice:
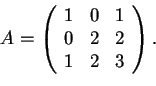
.
rispetto a
è lo spazio delle soluzioni del sistema omogeneo la cui matrice dei coefficienti è la stessa
, che è equivalente al sistema:
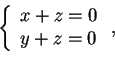
.


 Teoria
Teoria