Esercizi

2.
Sia $\mathbf{V}=\mathbf{C}^3$ e sia $\mathcal{B}=((1,0,i),(0,1,0),(0,0,i))$ una base. Si consideri $f \in Bils(\mathbf{V})$ così definita:

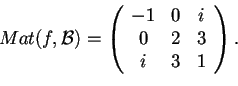
\begin{displaymath}Mat(f,\mathcal{B})= \begin{array}({ccc}) -1 & 0 & i\\ 0 & 2 & 3\\ i & 3 & 1 \end{array}. \end{displaymath}

e sia $q$ la forma quadratica associata a $f$.
a)
Si provi che il vettore $\mathbf{u}=(1,0,-i)_{\mathcal{B}}$ è isotropo, e che $\mathbf{v}=(0,i,1+i)_{\mathcal{B}}$ non lo è.
b)
Si provi che $<\mathbf{u}>+\mathbf{u}^{\perp}$ non è una somma diretta.
È vero che $<\mathbf{u}>+\mathbf{u}^{\perp}=\mathbf{V}$?
c)
Si decomponga $\mathbf{V}$ come $<\mathbf{v}>+\mathbf{v}^{\perp}$, e si determini la proiezione di $\mathbf{w}=(1,0,i)_{\mathcal{B}}$ su $<\mathbf{v}>$ rispetto a questa decomposizione.

Vuoi un aiuto?
Per vedere la soluzione totale, clicca , oppure clicca per visualizzare ogni singolo passo della soluzione.

Soluzione
Punto a)
Consideriamo la forma associata a $f$:
$q(x,y,z)=-x^2+2y^2+z^2+2ixz+6yz$;
e controlliamo:
$q((1,0,-i)_{\mathcal{B}})=-1-1+2=0$, quindi $\mathbf{u}$ è isotropo;
$q((0,i,1+i)_{\mathcal{B}})=-2+1+2i-1+6i-6=8i-8\neq0$, quindi $\mathbf{v}$ è non isotropo.
Punto b)   .
Per controllare se $<\mathbf{u}>\oplus\mathbf{u}^{\perp}$ si può procedere in diversi modi:
possiamo determinare dei vettori che generano $\mathbf{u}^{\perp}$ e vedere se la matrice le cui righe sono composte da questi vettori e dal vettore $\mathbf{u}$ ha rango massimo, oppure procedere così :
sappiamo che $\mathbf{u}$ è isotropo, quindi $f(\mathbf{u},\mathbf{u})=0$; ciò implica che $\mathbf{u} \in \mathbf{u}^{\perp}$, oltre che $\mathbf{u} \in <\mathbf{u}>$.
Allora $<\mathbf{u}> \cap \mathbf{u}^{\perp} \supseteq \{\mathbf{u}\} \,$ con $\, \mathbf{u}\neq0$; inoltre poiché $\mathbf{u}$ è isotropo, $\lambda \mathbf{u}$ è ortogonale a $\mathbf{u}, \,\, \forall \lambda \in \mathbf{C}, \,$ cioè $\, \lambda \mathbf{u} \in \mathbf{u}^{\perp} \,$ allora $\, <\mathbf{u}> \subseteq \mathbf{u}^{\perp}$.
Da ciò si deduce che la loro somma non è diretta. Abbiamo appena dimostrato che $<\mathbf{u}> \subseteq \mathbf{u}^{\perp}$, quindi
$<\mathbf{u}>+\mathbf{u}^{\perp}=\mathbf{u}^{\perp}$;
ma, essendo $f$ non degenere,
$\forall \mathbf{u}\in\mathbf{V}, \, \exists \mathbf{w} \in \mathbf{V} \,$ tale che $\, f(\mathbf{u},\mathbf{w}) \neq 0 \,\, \Rightarrow \mathbf{w} \notin \mathbf{u}^{\perp}$,
quindi è falso che $\mathbf{u}^{\perp}=\mathbf{V}$.
Punto c)   .
I passo:
Determiniamo $\mathbf{v}^{\perp}$:
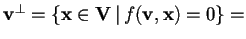
$\mathbf{v}^{\perp}=\{ \mathbf{x} \in \mathbf{V}\, \vert\, f(\mathbf{v},\mathbf{x})=0 \}=$
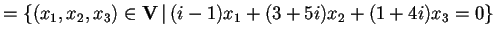
$=\{ (x_{1},x_{2},x_{3}) \in \mathbf{V}\, \vert\, (i-1)x_{1}+(3+5i)x_{2}+(1+4i)x_{3}=0 \}$
allora la condizione sul generico elemento di $\mathbf{v}^{\perp}$ sarà:

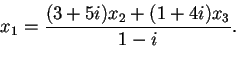
\begin{displaymath}x_{1}=\frac{(3+5i)x_{2}+(1+4i)x_{3}}{1-i}. \end{displaymath}

Allora otteniamo che $\mathbf{v}^{\perp}=<(\frac{3+5i}{1-i},1,0),(\frac{1+4i}{1-i},0,1)>$; quindi

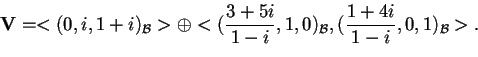
\begin{displaymath}\mathbf{V}=<(0,i,1+i)_{\mathcal{B}}>\oplus <(\frac{3+5i}{1-i},1,0)_{\mathcal{B}},(\frac{1+4i}{1-i},0,1)_{\mathcal{B}}>. \end{displaymath}

II passo:  
La proiezione di $\mathbf{w}=(1,0,i)_{\mathcal{B}}$ è:

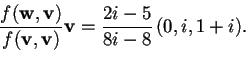
\begin{displaymath}\frac{f(\mathbf{w},\mathbf{v})}{f(\mathbf{v},\mathbf{v})}\mathbf{v}=\frac{2i-5}{8i-8}\,(0,i,1+i). \end{displaymath}