
Esercizi

- 2.
- Si consideri la base canonica su
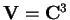 e
e
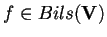 così definita:
così definita:
In ognuno dei seguenti casi si determini:
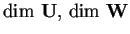 ,
e si dica se
,
e si dica se
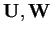 sono ortogonali oppure no.
sono ortogonali oppure no.
- a)
-
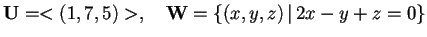 ;
;
- b)
-
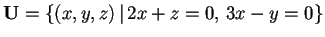 ,
,
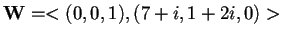 ;
;
- c)
-
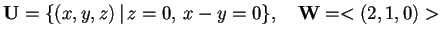 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
-
- Per vedere se due sottospazi sono fra loro ortogonali, procediamo così :
siano
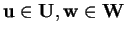 e calcoliamo
e calcoliamo
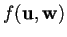 :
:
- -
- se
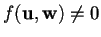 ,
i due sottospazi non sono ortogonali.
,
i due sottospazi non sono ortogonali.
- -
- se
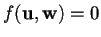 ,
ripeto l'operazione per tutti i vettori delle due basi di
,
ripeto l'operazione per tutti i vettori delle due basi di
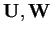 .
Se il risultato è sempre nullo, allora
.
Se il risultato è sempre nullo, allora
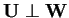 .
.
- Punto a)
-
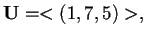 allora
allora
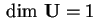 .
.
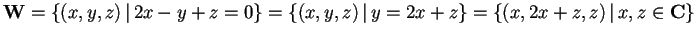
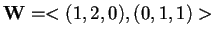 ,
quindi, poiché è un sottospazio generato da due vettori linearmente indipendenti fra loro,
,
quindi, poiché è un sottospazio generato da due vettori linearmente indipendenti fra loro,
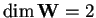 .
Ora, svolgendo i calcoli, otteniamo:
.
Ora, svolgendo i calcoli, otteniamo:
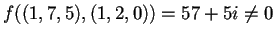
,
quindi
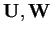 non sono ortogonali.
non sono ortogonali.
Punto
b)
-
-
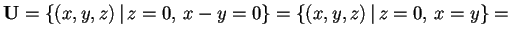
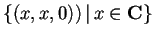 ,
,
allora
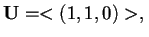 e
e
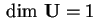 .
Inoltre
.
Inoltre
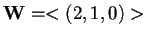 e
e
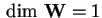 .
Per vedere se sono ortogonali:
allora
.
Per vedere se sono ortogonali:
allora
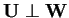 .
.




e
così definita:
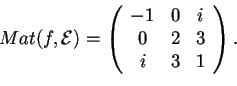
, e si dica se
sono ortogonali oppure no.
;
,
;
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzionee calcoliamo
:
, i due sottospazi non sono ortogonali.
, ripeto l'operazione per tutti i vettori delle due basi di
. Se il risultato è sempre nullo, allora
.
allora
.
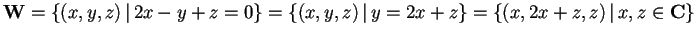
, quindi, poiché è un sottospazio generato da due vettori linearmente indipendenti fra loro,
. Ora, svolgendo i calcoli, otteniamo:
quindi,
non sono ortogonali.
.
allora
.
e, poiché i due vettori sono evidentemente linearmente indipendenti,
. Ora, si ha:
allora i due sottospazi non sono ortogonali fra loro.,
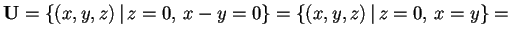
,
e
. Inoltre
e
. Per vedere se sono ortogonali:
allora.


 Teoria
Teoria