Esercizi

2.
Consideriamo la forma quadratica su $\mathbf{R}^3$,
$q(\mathbf{x})=-7h x_{1}^2+34x_{2}^2+3x_{3}^2+2hx_{1}x_{2}+2(h+k)x_{1}x_{3}-6hx_{2}x_{3}$;
per quali valori di $h,k ;\, \mathcal{C}=((\frac{1}{3},0,-\frac{1}{3}),(-\frac{2}{3},-1,\frac{11}{3}),(0,0,1))$ è una base diagonalizzante per $f$?

Vuoi un aiuto?
Per vedere la soluzione, clicca .

Soluzione
Una base è diagonalizzante per una forma simmetrica se la relativa matrice associata è diagonale.
Calcoliamo la matrice di $q$ rispetto alla base canonica; avremo

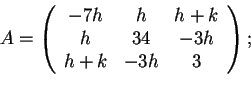
\begin{displaymath}A=\begin{array}({ccc}) -7h & h & h+k\\ h & 34 & -3h\\ h+k & -3h & 3 \end{array}; \end{displaymath}

rispetto alla base $\mathcal{C}$, diventa
$\begin{array}({ccc}) \frac{1}{3} & 0 & -\frac{1}{3}\\ -\frac{2}{3} & -1 & \f... ...frac{2}{3} & 0\\ 0 & -1 & 0\\ -\frac{1}{3} & \frac{11}{3} & 1 \end{array}=$
$\qquad$
$=\begin{array}({ccc}) -h-\frac{2}{9}k+\frac{1}{3} & \frac{15}{9}h+\frac{13}{9}... ...}{3}k+11\\ \frac{1}{3}(h+k)-1 & \frac{7}{3}h-\frac{2}{3}k+11 & 3 \end{array}$.
Affinché sia diagonale, occorre porre uguale a zero gli elementi che non occupano la diagonale principale, quindi: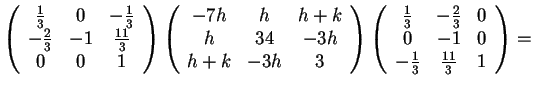
$\left\{ \begin{array}{l} \frac{1}{3}(h+k)-1=0\\ \frac{7}{3}h-\frac{2}{3}k+11=0\\ \frac{15}{9}h+\frac{13}{9}k-\frac{11}{3}=0 \end{array}\right.$ .
Risolvendo il sistema si ottiene che per $h=-3, \, k=6, \quad \mathcal{C}$ è diagonale per $q$.