

- 1.
- Consideriamo il polinomio
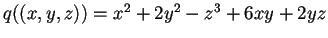 .
.
La matrice 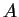 della relativa forma quadratica rispetto alla base canonica è:
della relativa forma quadratica rispetto alla base canonica è:
Ora vogliamo trovare un nuovo polinomio che rappresenti la stessa forma quadratica ma in una base diversa,
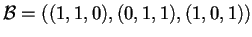 .
.
Tale matrice 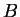 sarà congruente ad
sarà congruente ad 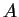 ,
e si otterrà considerando la matrice del cambiamento di base:
,
e si otterrà considerando la matrice del cambiamento di base:
di conseguenza,
Il nuovo polinomio sarà
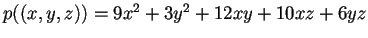 e le matrici
e le matrici 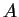 e
e 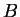 sono congruenti.
sono congruenti.
- 2.
- Sia
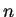 un intero positivo,
un intero positivo,
![$\mathbf{R}_{n}[x]$](img17.gif) lo spazio dei polinomi, la matrice
lo spazio dei polinomi, la matrice 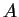 dell'applicazione bilineare:
dell'applicazione bilineare:
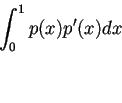 |
(1) |
rispetto alla base
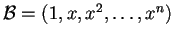 di
di
![$\mathbf{R}_{n}[x]$](img17.gif) ,
è una matrice quadrata di ordine
,
è una matrice quadrata di ordine 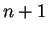 il cui elemento nella posizione
il cui elemento nella posizione 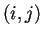 è
è
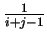 ,
cioè:
,
cioè:
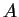 è simmetrica, quindi otteniamo la forma associata
è simmetrica, quindi otteniamo la forma associata 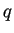 ponendo
ponendo
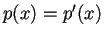 .
.




.
della relativa forma quadratica rispetto alla base canonica è:
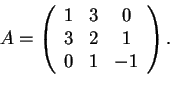
.
sarà congruente ad
, e si otterrà considerando la matrice del cambiamento di base:
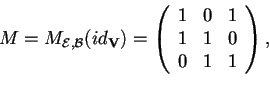
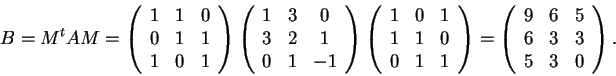
e le matrici
e
sono congruenti.
un intero positivo,
lo spazio dei polinomi, la matrice
dell'applicazione bilineare:
di
, è una matrice quadrata di ordine
il cui elemento nella posizione
è
, cioè:
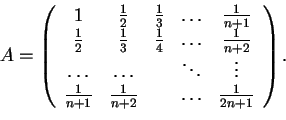
è simmetrica, quindi otteniamo la forma associata
ponendo
.

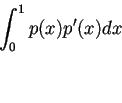

 Teoria
Teoria