Esercizi

Dimostrare che l'applicazione (2) è veramente una forma bilineare.

Vuoi un aiuto?
Per vedere la soluzione totale, clicca , oppure clicca per visualizzare ogni singolo passo della soluzione.

Soluzione.
I passo:
Prendiamo $\alpha,\beta \in \mathbf{R}, \quad \mathbf{u},\mathbf{u}',\mathbf{u}'' \in \mathbf{u}, \quad \mathbf{w},\mathbf{w}',\mathbf{w}'' \in \mathbf{V}$, allora
$(h \oplus k)(\alpha (\mathbf{u},\mathbf{w})+\beta (\mathbf{u}',\mathbf{w}'),(\m... ...\mathbf{u}',\alpha \mathbf{w} +\beta \mathbf{w}'),(\mathbf{u}'',\mathbf{w}''))=$
$=h(\alpha \mathbf{u} + \beta \mathbf{u}',\mathbf{u}'')+k(\alpha \mathbf{w} + \beta \mathbf{w}',\mathbf{w}'')=$ (per la bilinearità di $h,k$)
$=\alpha h(\mathbf{u},\mathbf{u}'')+ \beta h(\mathbf{u}',\mathbf{u}'')+\alpha k(\mathbf{w},\mathbf{w}'')+\beta k(\mathbf{w}',\mathbf{w}'')=$
$=\alpha (h(\mathbf{u},\mathbf{u}'')+k(\mathbf{w},\mathbf{w}''))+\beta (h(\mathbf{u}',\mathbf{u}'')+ k(\mathbf{w}',\mathbf{w}''))=$
$=\alpha (h\oplus k)((\mathbf{u},\mathbf{w}),(\mathbf{u}'',\mathbf{w}''))+\beta (h\oplus k)((\mathbf{u}',\mathbf{w}'),(\mathbf{u}'',\mathbf{w}''))$.
$(h \oplus k)((\mathbf{u},\mathbf{w}),\alpha(\mathbf{u}',\mathbf{w}')+\beta(\mat... ...(\alpha \mathbf{u}'+\beta \mathbf{w}',\alpha \mathbf{u}''+\beta \mathbf{w}''))=$
$=h(\mathbf{u},\alpha \mathbf{u}' + \beta \mathbf{u}'')+k(\mathbf{w},\alpha \mathbf{w}' + \beta \mathbf{w}'')=$ per la bilinearità di $h,k$
$=\alpha h(\mathbf{u},\mathbf{u}')+ \beta h(\mathbf{u},\mathbf{u}'')+\alpha k(\mathbf{w},\mathbf{w}')+\beta k(\mathbf{w},\mathbf{w}'')=$
$=\alpha (h(\mathbf{u},\mathbf{u}')+k(\mathbf{w},\mathbf{w}'))+\beta (h(\mathbf{u},\mathbf{u}'')+ k(\mathbf{w},\mathbf{w}''))=$
$=\alpha (h\oplus k)((\mathbf{u},\mathbf{w}),(\mathbf{u}',\mathbf{w}'))+\beta (h\oplus k)((\mathbf{u},\mathbf{w}),(\mathbf{u}'',\mathbf{w}''))$.
II passo:  
Verifichiamo il caso in cui $h,k$ sono forme simmetriche:
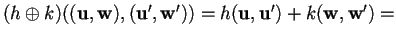
$(h \oplus k)((\mathbf{u},\mathbf{w}),(\mathbf{u}',\mathbf{w}'))=h(\mathbf{u},\mathbf{u}')+k(\mathbf{w},\mathbf{w}')=$
$=h(\mathbf{u}',\mathbf{u})+k(\mathbf{w}',\mathbf{w})=(h \oplus k)((\mathbf{u}',\mathbf{w}'),(\mathbf{u},\mathbf{w})$.