Esempio

Consideriamo la forma bilineare:
$\psi: \mathbf{R}^2 \times \mathbf{R}^2 \rightarrow \mathbf{R}, \qquad \psi(\mathbf{x},\mathbf{y})=2x_{1}y_{2}-3x_{2}y_{2}+x_{2}y_{1}$
e prendiamo $\mathcal{C}=((2,1),(0,1)) $ e $\, \mathcal{B}=((4,0),(2,2))$, due basi di $\mathbf{R}^2$.
Vogliamo verificare la relazione di congruenza esistente fra $Mat(\psi,\mathcal{C}) \,$ e $ \, Mat(\psi,\mathcal{B})$.
Le matrici associate a $\phi$ relative alle due basi saranno:

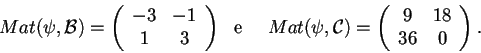
\begin{displaymath}Mat(\psi,\mathcal{B})= \begin{array}({ccc}) -3 & -1\\ 1 &... ...l{C})= \begin{array}({ccc}) 9 & 18\\ 36 & 0 \end{array}. \end{displaymath}

Prendiamo la matrice del cambiamento di base da $\mathcal{C}$ a $\mathcal{B}$, che si ottiene così
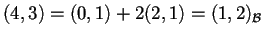
$(4,3)=(0,1)+2(2,1)=(1,2)_{\mathcal{B}}$
$(6,0)=-3(0,1)+3(2,1)=(-3,3)_{\mathcal{B}}$
allora

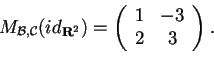
\begin{displaymath}M_{\mathcal{B,C}}= \begin{array}({ccc}) 1 & -3\\ 2 & 3 \end{array}. \end{displaymath}

Ora possiamo verificare la relazione studiata:
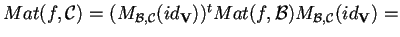
$Mat(f,\mathcal{C})= (M_{\mathcal{B,C}}(id_{\mathbf{V}}))^{t}Mat(f,\mathcal{C})M_{\mathcal{B,C}}(id_{\mathbf{V}})=$
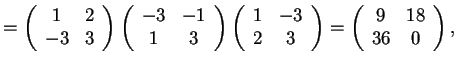
$=\begin{array}({ccc}) 1 & 2\\ -3 & 3 \end{array} \begin{array}({ccc}) -3 ... ...\\ 2 & 3 \end{array} =\begin{array}({ccc}) 9 & 18\\ 36 & 0 \end{array},$
che è proprio la matrice di $\psi$ rispetto a $\mathcal{B}$ calcolata sopra.