
Esercizi

Vuoi un aiuto?
- 2.
- Calcolare la forma bilineare su
associata alla matrice
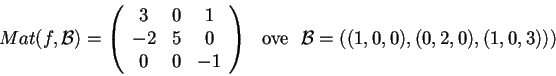
rispetto alla base canonica.
Per vedere la soluzione totale, clicca.
Soluzione
- 2.
- Per trovare
rispetto alla base canonica, basta applicare la formula per il cambiamento di base nelle forme bilineari:
Quindi dobbiamo determinare la matrice del passaggio dalla base.
alla base canonica
in
:
da cui si ha che:,
,
,
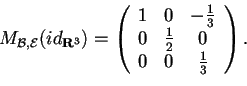
Sostituendo i valori ottenuti, abbiamo che
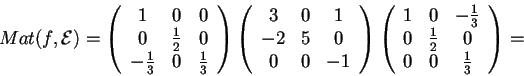
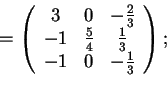
perciò la forma bilineare cercata è:
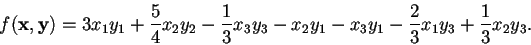


 Teoria
Teoria