Esempi

1.
-
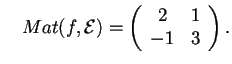
Sia $f \in Bil(\mathbf{R}^{2})$ tale che $\quad Mat(f,\mathcal{E}) = \begin{array}({cc}) 2 & 1\\ -1 & 3 \end{array}.$
Allora $r(f)=2$ e quindi $f$ è non degenere.
-
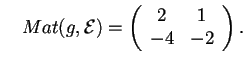
Sia invece $g \in Bil(\mathbf{R}^{2})$ tale che $\quad Mat(g,\mathcal{E}) = \begin{array}({cc}) 2 & 1\\ -4 & -2 \end{array}.$
In questo caso si ha $r(g)=1, $ quindi $g$ è degenere.
2.
Sia $f \in Bil(\mathbf{R}^{2}),\quad \mathcal{E}\,$ base per $\mathbf{R}^2$, con
$f((x_1,x_2)(y_1,y_2))=2x_1y_1+x-1y_2+x_2y_2$
quindi

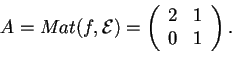
\begin{displaymath}A=Mat(f,\mathcal{E})= \begin{array}({cc}) 2 & 1\\ 0 & 1 \end{array}. \end{displaymath}

Sia $\mathbf{v}=(3,1)$ il vettore fisso dell'applicazione:
$h:=f(\mathbf{v},*):\mathbf{R}^{2} \rightarrow \mathbf{R}, $ con $(y_1,y_2) \rightarrow f((3,1),(y_1,y_2))$.
Allora la nuova applicazione è determinata dalla matrice $M_{\mathfrak{EE} }(h)=(6\quad 4)$ ottenuta da

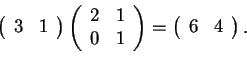
\begin{displaymath}\begin{array}({cc}) 3 & 1 \end{array} \begin{array}({cc}) ... ...& 1 \end{array} = \begin{array}({cc}) 6 & 4 \end{array}. \end{displaymath}