

- 2.
- Data la forma bilineare su
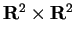 ;
sia
calcolare la matrice che esprime
;
sia
calcolare la matrice che esprime 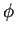 rispetto alla base
rispetto alla base
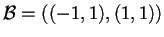 ,
,
- congruente a
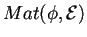 ,
attraverso la matrice cambiamento di base.
,
attraverso la matrice cambiamento di base.
Determinare poi la matrice che esprime 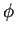 rispetto alla base
rispetto alla base
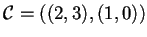 e
e
- verificare che
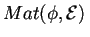 e
e
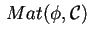 sono congruenti.
Perché?
sono congruenti.
Perché?
Vuoi un aiuto?
Per vedere la soluzione clicca .
Soluzione
.
Soluzione
- I passo:
- Iniziamo a calcolare
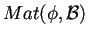 attraverso
la formula:
attraverso
la formula:
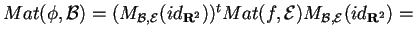
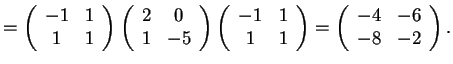
II passo:
Calcoliamo ora i vettori-base di
 rispetto
a
rispetto
a 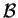 per costruire la matrice del cambiamento di base:
quindi svolgendo i calcoli troveremo che
per costruire la matrice del cambiamento di base:
quindi svolgendo i calcoli troveremo che
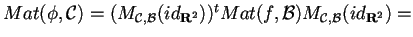
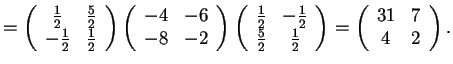
III passo:
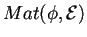 e
e
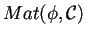 sono congruenti se e solo se esiste una matrice
sono congruenti se e solo se esiste una matrice 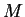 invertibile tale che
invertibile tale che
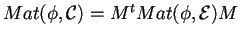
.
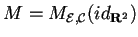 ,
questa verifica le condizioni richieste:
,
questa verifica le condizioni richieste:
è una matrice non degenere di rango massimo, quindi
è invertibile;
inoltre
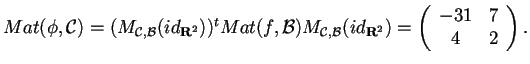
IV passo:
- Le tre matrici sono fra loro congruenti
poiché la
congruenza, essendo una relazione di equivalenza,
- gode della
proprietà transitiva.




; sia
calcolare la matrice che esprimerispetto alla base
,
, attraverso la matrice cambiamento di base.
rispetto alla base
e
e
sono congruenti. Perché?
. Soluzione
attraverso la formula:
rispetto a
per costruire la matrice del cambiamento di base:
quindi svolgendo i calcoli troveremo chee
sono congruenti se e solo se esiste una matrice
invertibile tale che
Quindi dobbiamo verificare che, presa.
, questa verifica le condizioni richieste:
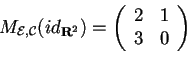
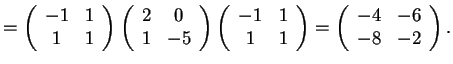
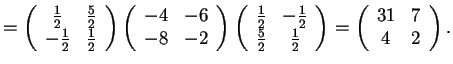
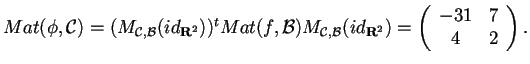

 Teoria
Teoria