Matematic@:
Derivate
|
|
|
|
Siano
Questo teorema generalizza il precedente (Lagrange), infatti ponendo Dimostrazione
Definiamo risulta quindi
possiamo quindi applicare il teorema di Rolle, cioè
e ciò conferma la tesi.
Per concludere la parte teorica enunciamo una regola utile per il calcolo di limiti di forme indeterminate Siano Se se e se
allora Dimostrazione
Dimostramo una versione semplificata della regola. Sfruttiamo delle ipotesi più forti ossia allora
Esempio
|
||
|
|
|
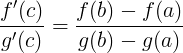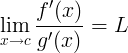
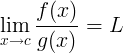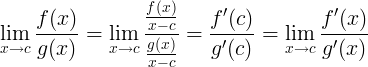e 
funzioni continue nell'intervallo [a,b] e derivabili nell'intervallo ]a,b[, con
, allora 
tale che 
.
otteniamo lo stesso risultato.
continua in [a,b] e derivabile su ]a,b[ con 
e 
con l'utilizzo delle derivate.
), sia 
;
,
tale che 
oppure se 
e 
.
e 
continue in c, 
e 
.
.