| |
Teorema di Rolle
Sia 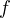 una funzione continua sull'intervallo chiuso [a,b] e derivabile sull'intervallo aperto ]a,b[, con una funzione continua sull'intervallo chiuso [a,b] e derivabile sull'intervallo aperto ]a,b[, con 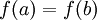 allora allora 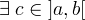 tale che tale che 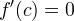 . .
 |
Si richiedono tali ipotesi per due motivi:
- Possiamo considerare il teorema di Rolle una sorta di caso particolare di quello di Weierstrass che garantisce la presenza di punti di massimo e minimo di una funzione continua su un intervallo chiuso.
- La derivabilità è richiesta solo sull'intervallo aperto in quanto cerchiamo punti di max/min all'interno dell'intervallo.
|
Torna all'indice
Teorema di Lagrange o del valore medio
Sia 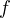 una funzione continua sull'intervallo chiuso [a,b] e derivabile sull'intervallo aperto ]a,b[, allora una funzione continua sull'intervallo chiuso [a,b] e derivabile sull'intervallo aperto ]a,b[, allora 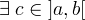 tale che tale che 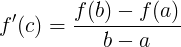 . .
Il teorema di Lagrange è una generalizzazione del teorema di Rolle.
Infatti non abbiamo più le ipotesi 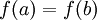 , ma sotto queste i due teoremi coincidono. , ma sotto queste i due teoremi coincidono.
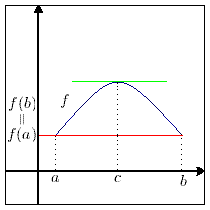
Graficamente il teorema di Lagrange indica che esiste, una volta soddisfatte le ipotesi, un punto in cui la tangente al grafico (gialla) è parallela alla retta passante per gli estremi del grafico (rossa). |
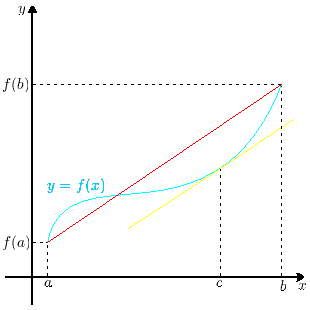 |
Dimostrazione
Consideriamo 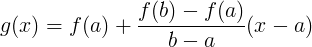 , ,
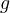 è continua in [a,b] e derivabile su ]a,b[ con è continua in [a,b] e derivabile su ]a,b[ con  e e 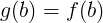 . .
Inoltre 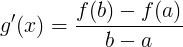 . .
Sia ora 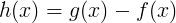 . .
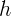 è anch'essa una funzione continua in [a,b] e derivabile su ]a,b[ con è anch'essa una funzione continua in [a,b] e derivabile su ]a,b[ con
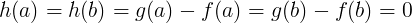
quindi possiamo applicare il teorema di Rolle ad 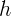 , allora , allora
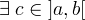 tale che tale che 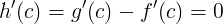
quindi 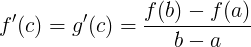 . .
Ciò conclude la dimostrazione.
Torna all'indice
|
|