CURVE CELEBRI |
 |
 |
 |
 |
 |
|
|
|
|||||
LA VERSIERA DI AGNESI
Storia
Questa curva si incontra nelle "Istituzioni analitiche ad uso della gioventù italiana" (1748) di Maria Gaetana Agnesi, dove essa viene designata col nome di versiera. Tuttavia l´equazione si trova già in un passo di Fermat (1666) che si occupò di quadrarla; ma il nome ora riferito alla curva, si trova per la prima volta nelle note al "Trattato del Galileo del moto naturalmente accelerato" (1718) di Guido Grandi, il quale fa riferimento al fatto che la curva fu ottenuta da lui stesso nell´opera "Quadratura circuli et hyperbolae" e dove si legge che il nome versiera deriva dal latino sinus versus, ovvero curva con seno verso, cioè contrario, nemico. Da qui versiera, "avversaria", che al tempo era il nome attribuito alle streghe. Questo spiega il fatto che la curva sia nota agli anglofoni come witch of Agnesi (strega di Agnesi).
Costruzione
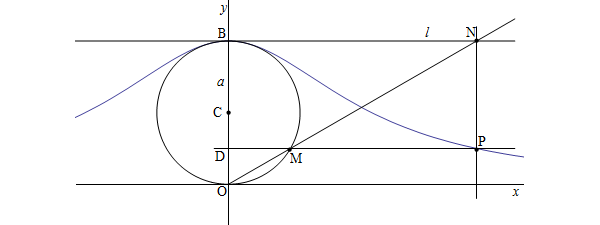
Riferendoci alla figura sopra, questa è la costruzione: per prima cosa tracciamo la circonferenza
di raggio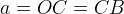 
e centro in 
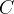situato a
distanza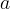 
dal centro degli assi. Sia 
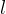una retta, parallela all´asse 
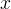e tangente alla circonferenza nel punto
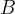a distanza 
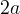dal centro degli assi.
Adesso tracciamo una linea passante per l´origine degli assi e un qualsiasi punto
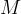della circonferenza. Questa retta intersecherà la retta
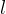in un punto 
.
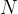Infine tracciamo una retta perpendicolare all´asse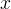
passante per il punto 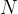. La versiera di Agnesi è il
luogo dei punti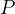 
intersezione di una retta parallela all´asse
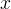e passante per
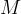e una retta perpendicolare all´asse 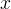e passante per
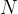al variare del punto 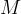sulla circonferenza.
Questa costruzione è la stessa che Maria Gaetana Agnesi fa (in termini più moderni)
nella sua opera sopra citata.
Equazioni
Dalla costruzione precedente si nota che i due triangoli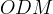 
e
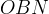sono triangoli simili e quindi si deduce:
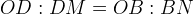
Sempre dalla figura si nota che possiamo sostituire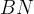 
con
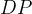essendo di uguale lunghezza. Detta
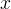tale lunghezza, 
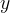quella del segmento
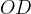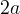, il diametro
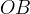, si ottiene per il teorema di Euclide che il segmento
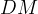è uguale a 
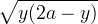poichè medio proporzionale tra i segmenti 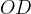e
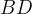. Con queste notazioni la proporzione scritta sopra diventa:
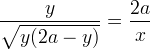
da cui si ricava l´equazione cartesiana della versiera:
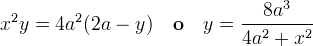
Da ciò si evince che la versiera è una cubica razionale avente l'asse delle
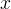come asintoto d´inflessione il che significa che la curva si avvicina all´
asintoto dopo aver incontrato due flessi nei punti di coordinate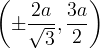 
.
Facilmente, poi, si ottengono le seguenti equazioni parametriche:
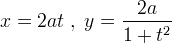
Proprietà
La versiera di Agnesi è una curva con numerose proprietà interessanti. Vediamone le principali:
-
l'area tra la versiera ed il suo asintoto è quattro volte l´area della circonferenza usata per descriverla, ovvero
; -
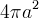il volume di rotazione della versiera intorno al proprio asintoto è due volte quella del volume di rotazione della circonferenza intorno all´asse
,
cioè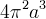 
; -
Il baricentro della curva si trova esattamente nel centro della circonferenza usata per descriverla;
-
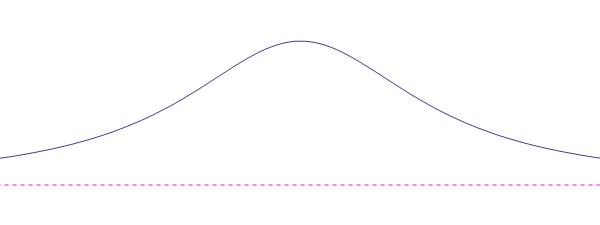
la curva si manifesta in teoria della probabilità come distribuzione di Cauchy
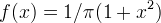, la cui equazione, a parte per una costante moltiplicativa di
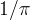, è quella della versiera con
; -
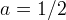la versiera trova molte applicazioni in fisica, soprattutto nei fenomeni di risonanza. La risonanza si verifica quando un´oscillazione esterna è esercitata su un sistema, con una frequenza nelle vicinanze di una certa "frequenza di risonanza". Un esempio è la luce monocromatica diretta che colpisce un atomo: l´intensità della radiazione emessa dall'atomo ha la forma di una versiera come funzione della differenza di frequenza (tra quella esterna e quella di risonanza). Altre applicazioni si trovano nei circuiti elettrici e in fluidodinamica.