LA TRATTRICE DI HUYGENS

 

 

Storia

Verso la fine del XVII° secolo il medico francese Claude Perrault, propose ai matematici dell´epoca una sfida, chiedendo quale fosse quella curva descritta in un piano da un punto pesante attaccato all´estremo di un filo teso, di cui l´altro estremo percorre una retta situata sullo stesso piano. Leibeniz studiò la curva risultante, ma fu Huygens il primo a definirla completamente battezzandola trattrice (dal latino trahere=trainare) o traiettoria di Huygens, mentre Ribaucour propose il nome di alisoide (a forma di giglio). La curva trovò nuovo interesse tra i matematici del XIX° secolo, in special modo Beltrami e Dini, quando modelli tridimensionali di geometrie non-euclidee iperboliche furono generati proprio grazie alla trattrice.

 

 

Descrizione

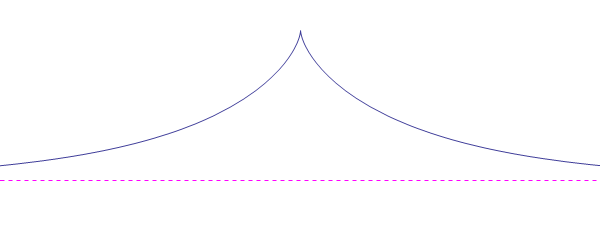
La trattrice viene solitamente descritta così: essa è il luogo dei punti tali che il segmento della tangente in un punto qualunque, compreso fra il punto di contatto e l´intersezione con una retta fissa, ha lunghezza costante. Un altro modo per descriverla è quella di considerare un cane (punto nero) che viene trascinato dal suo padrone tramite un guinzaglio lungo un percorso rettilineo: il cane percorrerà una trattrice.

 

 

 

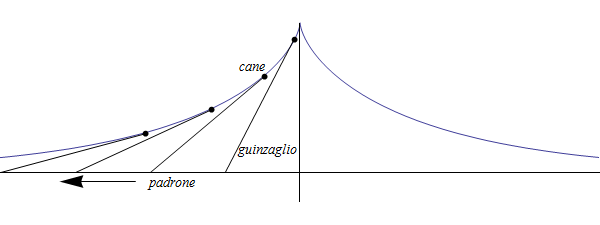
Equazioni

La trattrice è una curva trascendente e le sue equazioni parametriche sono:

 

 

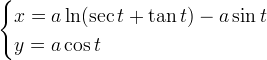
dove 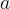è la lunghezza del "guinzaglio". La trattrice ammette anche la seguente equazione cartesiana:

 

 

 

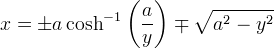
Proprietà

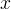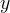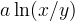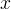Per prima cosa vediamo alcune proprietà metriche della curva: la lunghezza di un arco di uno dei due rami fra i punti e vale ; l´area compresa tra la trattrice e il suo asintoto, che è l´asse , è .

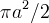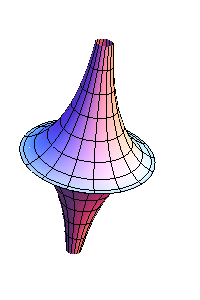
La più grande applicazione della trattrice fu lo studio abbinato alle geometrie non-euclidee: più precisamente Beltrami e Dini crearono due modelli tridimensionali di geometria iperbolica. Beltrami ideò la pseudosfera, così chiamata poichè ammette curvatura costante opposta a quella della sfera in ogni suo punto e quindi negativa. La pseudosfera è generata da una rotazione attorno al proprio asse della trattrice (figura a sinistra). L´altro modello di geometria iperbolica è dato dalla superfice del Dini, ovvero la superficie laterale del solido ottenuto assegnando alla trattrice un moto elicoidale intorno al suo asintoto (figura a destra).
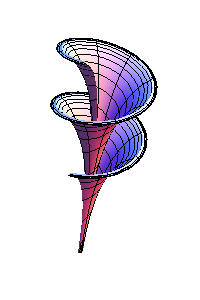