LA STROFOIDE RETTA
Storia
La strofoide si trova descritta nella corrispondenza di Evangelista Torricelli, intorno al 1645, anche se sembra sia stata studiata precedentemente dal matematico francese de Roberval. Ci fu una disputa tra i due su alcune scoperte, ed in particolare anche sulla strofoide; tutto ciò era dovuto al fatto che entrambi stavano lavorando agli stessi argomenti appartenendo al circolo che faceva capo a padre Mersenne, ed è dunque probabile siano arrivati contemporanemente alle stesse scoperte indipendentemente. La curva fu anche studiata da Barrow, intorno al 1670, il quale fu il maestro di Newton. Il nome strofoide, fu coniato da uno scrittore francese, Montucci, nel 1846, e deriva dal greco strophos che significa "cintura con anello atto a portare la spada". Per le numerose proprietà in relazione con i logaritmi ed il cerchio, la curva viene detta "logociclica"; inoltre per alcune proprietà collegate alla nozione di gruppo armonico, viene anche detta "armonica".
Costruzione
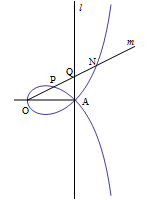
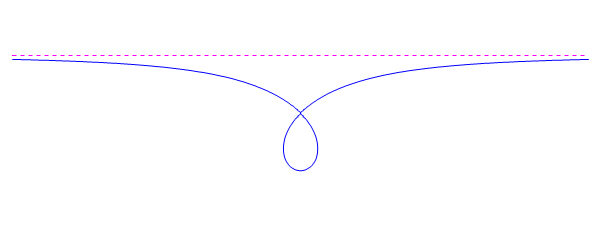
Vediamo come costruire la curva: sia data una retta
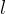 ed un punto
ed un punto 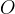 che chiameremo polo. Ora
consideriamo la perpendicolare alla retta
che chiameremo polo. Ora
consideriamo la perpendicolare alla retta 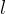 passante per il punto
passante per il punto
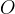 , la quale intersecherà la retta nel punto
, la quale intersecherà la retta nel punto
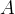 . Tracciamo ora una linea
. Tracciamo ora una linea 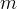 partente dal punto
partente dal punto
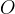 che taglierà la retta
che taglierà la retta 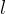 nel punto
nel punto
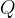 . Chiameremo strofoide retta il luogo dei
punti
. Chiameremo strofoide retta il luogo dei
punti 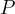 e
e 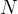 tali che si abbia:
tali che si abbia:
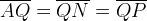 . Questa descrizione porta ad una
strofoide così detta retta, per distinguerla dalla
strofoide obliqua la cui costruzione muta solo nella scelta del punto
. Questa descrizione porta ad una
strofoide così detta retta, per distinguerla dalla
strofoide obliqua la cui costruzione muta solo nella scelta del punto
 , non più ai piedi della perpendicolare ad
, non più ai piedi della perpendicolare ad
 , ma in un qualsiasi altro punto sulla retta stessa.
, ma in un qualsiasi altro punto sulla retta stessa.
In realtà de Roberval, a quanto pare, trovò la curva come risultato di un piano che taglia un cono: quando il piano ruota (rispetto alla tangente al vertice del cono) il luogo dei fuochi della conica ottenuta dà la strofoide.
Equazioni
Facendo riferimento alla figura precedente, considerate le coordinate
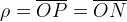 e
e 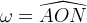 , si ottiene la
seguente equazione polare, preso come centro
, si ottiene la
seguente equazione polare, preso come centro 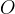 e
e
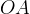 come asse:
come asse:
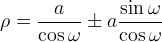
dove 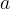 è la lunghezza del segmento
è la lunghezza del segmento 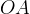 .
Le sostituzioni standard per
.
Le sostituzioni standard per 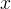 e
e
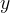 danno la seguente equazione cartesiana:
danno la seguente equazione cartesiana:
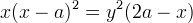
se prendiamo per centro il punto degli assi il punto 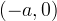 , si ottiene
la più usuale forma di equazione cartesiana:
, si ottiene
la più usuale forma di equazione cartesiana:
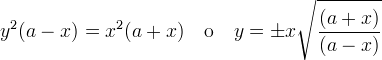
nel primo caso la retta 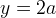 è l´asintoto nel secondo caso
lo è la retta
è l´asintoto nel secondo caso
lo è la retta 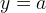 .
.
Proprietà

Vediamo alcune proprietà metriche della curva: l´area all´interno del "loop" è di
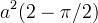 mentre l´area tra la curva e l´asintoto vale
mentre l´area tra la curva e l´asintoto vale
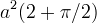 . Abbiamo detto che quella descritta è la
strofoide retta. L´aggettivo retta sta ad indicare che nella costruzione abbiamo preso la linea
direttrice perpendicolare al segmento
. Abbiamo detto che quella descritta è la
strofoide retta. L´aggettivo retta sta ad indicare che nella costruzione abbiamo preso la linea
direttrice perpendicolare al segmento 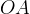 ; se prendiamo una retta obliqua, dalla
costruzione risulterà un strofoide obliqua (come si vede in figura sopra). In realtà si
può generalizzare ancora di più la costruzione trovando diverse curve: ad esempio se al posto della retta direttrice
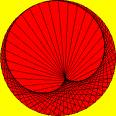
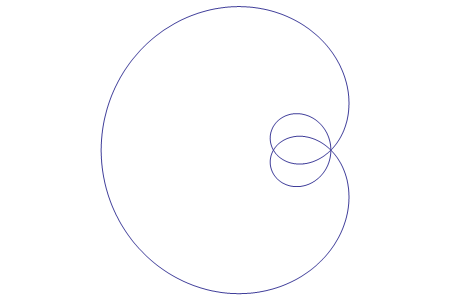
si usa una circonferenza con polo nel suo centro, si ottiene la cosiddetta strofoide (o nefroide)
di Freeth; il matematico inglese se ne servì per la costruzione di un eptagono regolare.
Variando il parametro
; se prendiamo una retta obliqua, dalla
costruzione risulterà un strofoide obliqua (come si vede in figura sopra). In realtà si
può generalizzare ancora di più la costruzione trovando diverse curve: ad esempio se al posto della retta direttrice
si usa una circonferenza con polo nel suo centro, si ottiene la cosiddetta strofoide (o nefroide)
di Freeth; il matematico inglese se ne servì per la costruzione di un eptagono regolare.
Variando il parametro 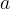 la curva può essere utilizzata per costruire poligoni
regolari a 9 e 11 lati. Curiose anche le strofoidi aventi polo all´infinito: un esempio ne
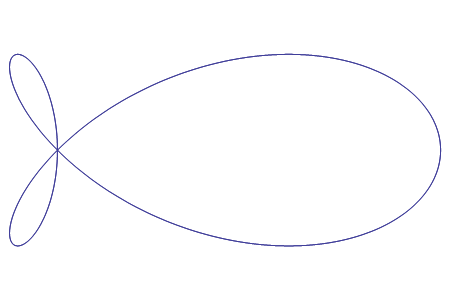
è la strofoide a tre petali relativa ad una cerchio con polo sulla circonferenza (sotto a
sinistra la strofoide di Freeth, a destra la strofoide a tre petali).
Ricordiamo inoltre che la strofoide può essere ottenuta come cissoide di una circonferenza, di
una retta passante per il centro della circonferenza e polo sulla circonferenza.
la curva può essere utilizzata per costruire poligoni
regolari a 9 e 11 lati. Curiose anche le strofoidi aventi polo all´infinito: un esempio ne
è la strofoide a tre petali relativa ad una cerchio con polo sulla circonferenza (sotto a
sinistra la strofoide di Freeth, a destra la strofoide a tre petali).
Ricordiamo inoltre che la strofoide può essere ottenuta come cissoide di una circonferenza, di
una retta passante per il centro della circonferenza e polo sulla circonferenza.
|
|