LA LEMNISCATA DI BERNOULLI

 

 

Storia

La lemniscata fu descritta dal grande matematico svizzero Jakob Bernoulli, da cui prende il nome, nell´Acta Eruditorum (giornale scentifico tedesco) nel 1694. Tuttavia egli non era a conoscenza del fatto che 14 anni prima l´italiano Giovanni Cassini, nella ricerca della traiettoria relativa della terra intorno al sole, aveva studiato una famiglia di curve, chiamate ovali di Cassini, di cui la lemniscata di Bernoulli era un caso particolare. Nel 1750 Giovanni Fagnano scoprì altre proprietà della curva, le quali appena un anno dopo portarono Eulero a porre le basi per lo studio delle funzioni ellittiche. Anche McLaurin, Abel e Watt si interessarono alla curva. Il nome lemniscata fu dato alla curva proprio da Bernoulli, e deriva dal latino lemniscus che nell´antica Roma era un nastro pendente dalle corone.

 

 

Costruzione

 

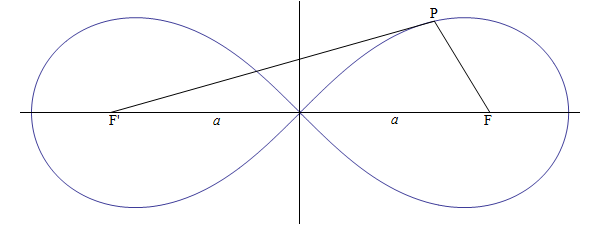
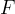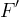La lemniscata fu descritta da Bernoulli, come variazione del metodo di costruzione di un ellisse; infatti, mentre quest´ultima è il luogo dei punti per cui la somma delle distanze da due punti fissi, detti fuochi, è costante, la lemniscata è il luogo dei punti per i quali il prodotto di queste distanze è costante. Detti e i fuochi, 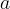la loro distanza dal centro, la lemniscata di Bernoulli è il luogo dei punti tali che:

 

 

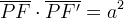
dove 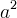è la costante, ovvero il quadrato della semi distanza tra i due fuochi.

 

 

Equazioni

La lemniscata di Bernoulli è una quartica razionale (ovvero ammette una equazione algebrica di quarto grado) con un punto doppio nodale nel centro, cioè nel punto alla stessa distanza dai due fuoci. La sua equazione algebrica è:

 

 

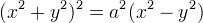
da cui, con i noti cambiamenti di coordinat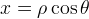e e 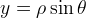, si ottiene facilmente la seguente equazione polare:

 

 

 

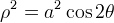
Proprietà

 

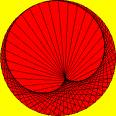
Come abbiamo detto la lemniscata è un caso particolare di ovali di Cassini, luogo dei punti i cui prodotti delle distanze dai fuochi è costante: nel caso particolare della lemniscata questa costante è uguale al quadrato della semi distanza tra i fuochi; se la costante è maggiore si ottengono degli ovali, se minore si ottengono due figure simili a piccole gocce fino ad arrivare al caso di due circonferenze. Inoltre, come si può vedere dalla figura sopra, gli ovali di Cassini sono le curve risultanti dalle intersezioni di un toro, con un piano parallelo all´asse di rotazione: in particolare la lemniscata di Bernoulli è l´intersezione di un toro con un piano parallelo all´asse di rotazione e tangente al punto interno del toro.

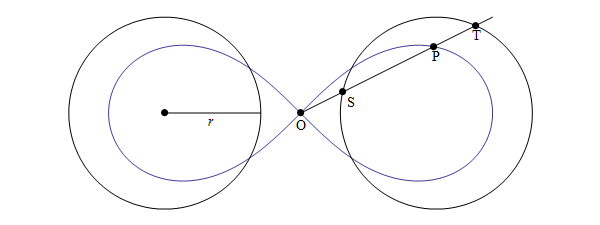
Un´altra proprietà della lemniscata di Bernoulli è quella di essere la cissoide di due circonferenze (come si può vedere sotto): siano date due circonferenze di raggio e sia 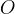il punto centrale del segmento congiungente i due centri delle circonferenze ad una distanza maggiore di da entrambi. Ora tracciamo una retta passante per il punto 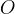e una delle due circonferenze (in questo modo si traccia uno dei due loop della lemniscata, l´altro è simmetrico rispetto ad 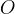) e siano 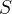e 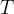le intersezioni con essa. Il luogo dei punti 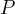tali ch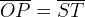e è la lemniscata di Bernoulli costruita con il metodo della cissoide.