IL FOLIUM DI CARTESIO

 

 

Storia

Il primo cenno al folium si ha in una lettera che Cartesio scrisse nel Gennaio 1638 a padre Mersenne affinché ne parlasse a Fermat, poiché secondo lo stesso Cartesio a questa curva non era applicabile il metodo delle tangenti del senatore tolosano. Per tutta risposta Fermat nell´Agosto dello stesso anno scrisse a Cartesio dimostrando il contrario e parlando per la prima volta della curva come "feuille" (foglia). In una lettera del settembre 1693 Huygens scrive a Leibniz parlando della curva come "feuille de Mr. des Cartes" (ovvero la "foglia di Cartesio"). A diffondere il nome di "folium di Cartesio" furono dapprima de Moivre che ne parla nel suo "Storia dell´Accademia delle Scienze" nel 1706 e soprattutto d´Alembert che dedicò alla curva un articolo speciale chiamandola con il nome oggi attribuitole, nella "Enciclopedia metodica". Il nome folium, che significa foglia, fu dato alla curva per la forma del suo "cappio" nel primo quadrante, non considerando il resto della curva, anzi pensando erroneamente che il cappio si ripetesse su tutti e quattro i quadranti.

 

 

Descrizione

Il folium di Cartesio è una curva del quale lo stesso Cartesio ignorava la costruzione per punti: infatti come abbiamo detto, non considerando all´epoca le coordinate negative, egli pensava si ripetesse il "cappio" in tutti e quattro i quadranti. Il folium è caratterizzato dalla proprietà che per ogni punto della curva la somma dei cubi delle coordinate cartesiane ortogonali è uguale al parallelepipedo rettangolo avente per spigoli le coordinate stesse ed una lunghezza data.

 

 

Equazioni

Se chiamiamo 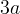la lunghezza data, il folium di Cartesio ha per equazione cartesiana:

 

 

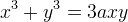
Tramite il ben noto cambiamento di coordinat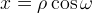e e 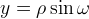si ottiene la seguente equazione polare:

 

 

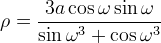
Infine le equazioni parametriche sono:

 

 

 

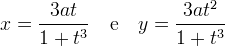
Proprietà

Il folium di Cartesio è una curva con non molte proprietà. Inannzi tutto essa è simmetrica rispetto alla diagonale del primo e terzo quadrante ed ha come asintoto la rett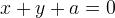a . Un´altra proprietà curiosa è che l´area del cappio è uguale all´area della regione del piano compresa fra l´asintoto e i rami infiniti della curva: entrambe sono uguali a 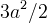.