LA CLOTOIDE

 

 

Storia

Il primo ad occuparsi della curva fu il grande matematico Leonhard Eulero, nel 1744, risolvendo un problema proposto da Giacomo Bernoulli, e per questo motivo la curva è spesso nota con il nome di spirale di Eulero. Più di un secolo dopo, nel 1874, il fisico francese Marie-Alfred Cornu, utilizzò la curva nelle sue ricerche sui fenomeni di diffrazione, e per questo talvolta è anche chiamata spirale di Cornu. Agli inizi del 1900, il matematico italiano Ernesto Cesaro le diede finalmente il nome di clotoide, in onore della Parca Cloto, dea latina, che filava lo stame della vita, avvolgendola sul fuso: un immagine che la clotoide ricorda chiaramente.

 

 

Descrizione

Il problema posto da Bernoulli era quello di trovare una curva, la cui curvatura in ogni singolo punto fosse proporzionale alla lunghezza dell´arco. Questo significa che più la curva si allontana dall´origine, pił essa ruota: una curva di questo tipo non può che essere una spirale. Eulero identificò che questa curva doveva essere la clotoide. Si può dare anche una definizione cinematica: la clotoide è la curva che, percorsa a velocità costante, è tale che la curvatura varia proporzionalmente al tempo.

 

 

Equazioni

La clotoide è una curva trascendente, ed ammette le seguenti equazioni parametriche:

 

 

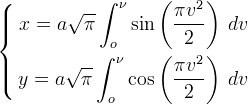
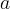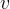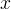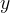dove è una costante di proporzionalità. Gli integrali che compaiono nelle formule sono i ben noti integrali di Fresnel. Dalle equazioni si vede che sostituendo a valori uguali e di segno contrario, corrispondono valori della e uguali e di segno contrario; questo dimostra che la curva è simmetrica rispetto all´origine.

 

 

Proprietà

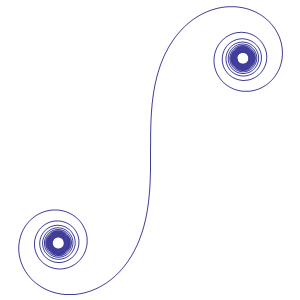
La clotoide è una curva simmetrica rispetto all´origine come detto e proprio nell´ origine ammette un flesso; inoltre i 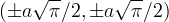punti sono detti punti asintotici della curva poichè i due rami si avvolgono all´infinito su questi due punti.

Due le applicazioni principali della clotoide. La prima in fisica, poichè essa descrive la diffrazione di un onda (ed in particolare della luce) dal bordo di un semipiano. La seconda nella vita reale: infatti per evitare il brusco passaggio da un tratto a curvatura nulla (rettilineo) ad un tratto a curvatura data (per esempio un arco di cerchio con raggio assegnato), nelle strade, nelle ferrovie e anche negli ippodromi, si inseriscono archi di clotoide come elementi di transizione.