LA CICLOIDE
Storia
Pur non essendo una curva di difficile concezione, sembra che la cicloide non sia venuta alla luce fino al XVI° secolo. Fu Pascal il primo a scoprirne le innumerevoli proprietà e a meravigliarsi che gli antichi greci l´avessero ignorata, anche se Giamblico (filisofo greco del III° secolo d.C.) sembra attribuire una curva simile a Carpo d´Antochia una curva "a doppio movimento" inventata per quadrare il cerchio. Tutto ciò non basta ad annoverare la curva tra quelle conosciute nell´antichità. Mersenne ne diede la prima definizione documentata; nei primi del 1600, Galileo Galilei fu il primo ad attribuirgli il nome che oggi le diamo. Nel 1634 Roberval risolse il problema dell´area compresa tra un arco della curva (da lui chiamata trocoide dal greco trocos=ruota) e la base, che aveva visto impegnati per circa 40 anni Torricelli e Galileo; Cartesio e Fermat trovarono le tangenti alla cicloide, ma fu Pascal, come detto, tornato ad occuparsi di matematica dopo un lungo periodo in cui si dedicò a religione e filosofia, a risvegliare grande interesse nella curva (da lui chiamata roulette) proponendo diverse sfide matematiche riguardanti la cicloide, a cui parteciparono i più grandi matematici dell´epoca: Wallis, Sluze, Fermat, Huygens, Ricci. Successivamente, scenziati del calibro dei fratelli Bernoulli, Leibniz e Newton trovarono per la curva famossisime proprietà matematiche e fisiche.
Descrizione
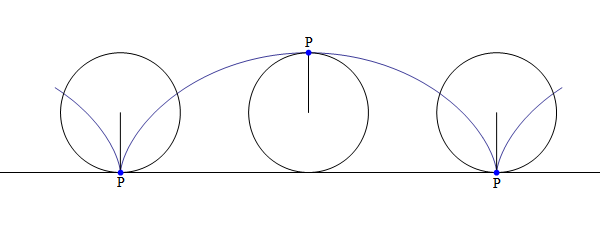
La cicloide è definita come il luogo dei punti 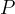 su
una circonferenza data che rotola senza strisciare su una retta. Questo tipo di cicloide viene detta
ordinaria. Se il punto
su
una circonferenza data che rotola senza strisciare su una retta. Questo tipo di cicloide viene detta
ordinaria. Se il punto 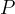 non si trova sulla circonferenza, si
parla di cicloide accorciata se il punto è interno e di
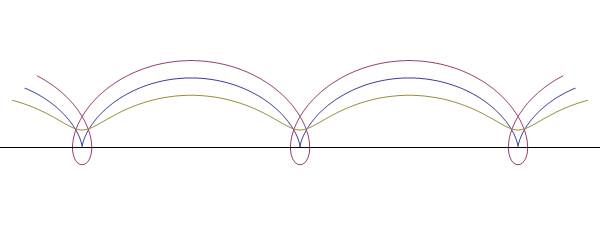
cicloide allungata se il punto è al di fuori della circonferenza: in basso è possibile
vedere il confronto tra le tre curve (cicloide ordinaria in blu, cicloide
accorciata in senape, cicloide allungata in viola).
non si trova sulla circonferenza, si
parla di cicloide accorciata se il punto è interno e di
cicloide allungata se il punto è al di fuori della circonferenza: in basso è possibile
vedere il confronto tra le tre curve (cicloide ordinaria in blu, cicloide
accorciata in senape, cicloide allungata in viola).
Equazioni
Dalla descrizione precedente si arriva facilmente alle equazioni parametriche della curva:
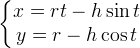
dove  è il raggio della circonferenza e
è il raggio della circonferenza e 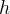 è la distanza del punto
è la distanza del punto 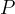 dal centro della circonferenza (alla partenza). Se
dal centro della circonferenza (alla partenza). Se
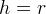 si ottiene la cicloide ordinaria, se
si ottiene la cicloide ordinaria, se
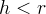 si ottiene la cicloide accorciata, infine la
cicloide allungata se
si ottiene la cicloide accorciata, infine la
cicloide allungata se 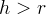 . Alla semplicità delle equazioni
parametriche si contrappone la più complessa equazione cartesiana ottenuta eliminando il parametro:
. Alla semplicità delle equazioni
parametriche si contrappone la più complessa equazione cartesiana ottenuta eliminando il parametro:
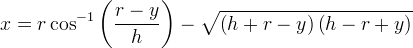
Proprietà
La cicloide è una curva con moltissime proprietà, le quali furono al centro di
innumerevoli dispute tra gli scienziati dell´epoca, tanto che la curva fu definita "la Elena della geometria".
Vediamo per prima cosa le proprietà metriche: l´area sottostante un ramo di cicloide
è tre volte l´area del cerchio usato per generarla ovvero 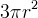 ; la lunghezza di un
arco di cicloide è quattro volte il diametro usato per descriverla.
; la lunghezza di un
arco di cicloide è quattro volte il diametro usato per descriverla.
Tuttavia le proprietà fisico-matematiche che hanno scatenato le più accese sfide tra gli scenziati di quel periodo sono le seguenti:
-
un pendolo che percorre una traiettoria cicloide è isocrono (dal greco isos=uguale e chronos=tempo), ovvero il suo periodo rimane costante indipendentemente dall´ampiezza delle sue oscillazioni.
-
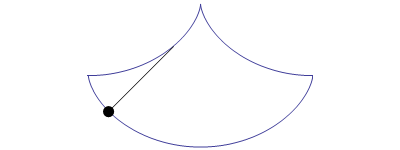
una scodella di forma cicloidale è tautocrona (dal greco tauto=identico e chronos=tempo), poichè uguali oggetti (tipo sferette) poste a varie altezze del recipiente raggiungeranno il fondo nello stesso tempo. Le due proprietà sono simili e fu Huygens da accorgersi di entrambe, precedentemente si pensava fosse la circonferenza ad avere queste due proprietà, ed in effetti per piccole oscillazioni la cicloide è approssimabile ad una circonferenza. Sotto possiamo vedere un esempio della proprietà tautocrona della cicloide (a sinistra) e del pendolo isocrono di Huygens (a destra): per costruirlo Huygens si avvalse di un´altra proprietà della cicloide e cioè che la sua evoluta (il luogo dei centri di curvatura) è ancora una cicloide, e quindi costruì due ganasce a forma di archi cicloidali rovesciati che si incontrano in una cuspide.

|
|
-
la cicloide ha la proprietà brachistocrona (dal greco brachistos=più corto e chronos=tempo): infatti essa è la curva su cui una massa che scivola impiega meno tempo per percorrere il tragitto fra due punti dati. I primi ad accorgersene furono i fratelli Bernoulli, che sembra litigarono per la scoperta, confutando il pensiero più intuitivo che fosse una retta collegante i due punti il percorso più breve.
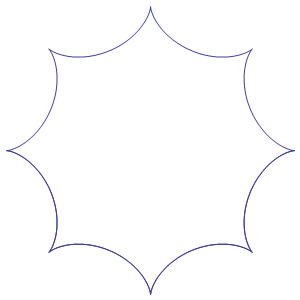
Infine, la cicloide si presta a innumerevoli generalizzazioni: se ad esempio al posto di una retta sul quale far scorrere la circonferenza si considera una seconda circonferenza (più grande di quella che scorre), le curve descritte verranno dette epicicloidi, se la circonferenza rotola esternamente, ipocicloidi, se la circonferenza rotola internamente. Ulteriori generalizzazioni si possono ottenere nel caso che il punto sia interno od esterno alla circonferenza. Sotto possiamo vedere un esempio di una epiciloide (a sinistra) e di una ipocicloide (a destra).

|
|