LA CATENARIA

 

 

Storia

Il primo ad occuparsi della catenaria fu Galielo Galilei, nel 1638, erroneamente pensando che la forma di una fune appesa per i suoi estremi e sotto la forza di gravità, fosse una parabola. Successivamente Joachim Jungius, nel 1669, dimostrò che non era la parabola la curva in questione. Nel 1691, quasi contemporaneamente, Huygens, Leibeniz e i fratelli Bernoulli, dimostrarono che tale curva era una curva non algebrica, e fu battezzata dallo stesso Huygens, catenaria (che deriva da catena, in riferimento alla caratterizzazione della curva). La curva, anche detta funicolare o velaria, fu studiata da Eulero il quale scoprì che la sua rotazione, attorno all´asse 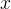, genera una superficie minima tra due circonferenze uguali.

 

 

Descrizione

 

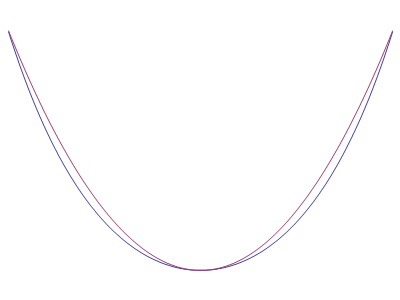
La catenaria è la forma di una fune ideale appesa per due punti. Per "fune ideale" si intende che la fune è perfettamente flessibile, inestensibile, senza spessore e con densità uniforme. Galileo confuse la curva con la parabola ed effettivamente vicino al vertice, catenaria (in blu) e parabola (in viola) sono quasi coincidenti, ed è quindi comprensibile l´errore di Galileo. Le due curve tuttavia sono differeneti se costituite da materiale pesante: nella catenaria la distribuzione del peso è uniforme per ogni lunghezza d´arco.

 

 

Equazioni

 

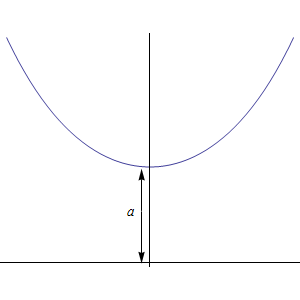
La catenaria è una curva trascendente che ammette la seguente equazione cartesiana:

 

 

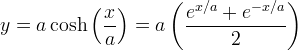
dove 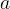è una costante che rappresenta la distanza del punto più basso con il "terreno". Dall´equazione si nota che la curva non dipende dalla distanza dei punti a cui è appesa la fune. Inoltre la curva è simmetrica rispetto all´asse .

 

 

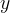Proprietà

 

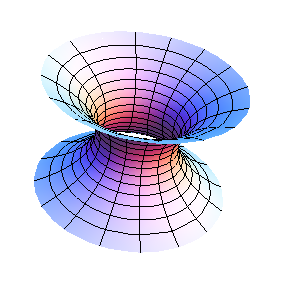
La catenaria ha moltissime applicazioni in tanti campi. Per prima cosa come detto in precedenza Eulero trovò che la superficie laterale del solido di rotazione generato da una catenaria che ruota attorno all´asse 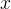, la catenoide, è la superficie minima tra due circonferenze della stessa grandezza. La superficie di rotazione della catenaria è l´unica superfice di rotazione, insieme al piano, ad essere superficie minima; questo si può vedere immergendo in una vasca piena di acqua e sapone due circonferenze uguali distanziate: la bolla di sapone che si formerà si disporrà per avere superficie minima e questa avrà proprio la forma di una catenoide.

Anche la sezione orizzontale di una vela sotto l´azione del vento assume la forma di una catenaria, e per questo la curva è anche nota come velaria.

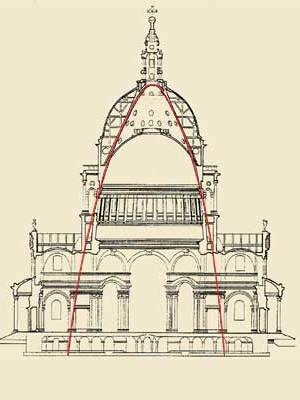
Numerose infine sono le applicazioni in vari ambiti dell´architettura: infatti, poichè la catenaria ha la proprietà di di avere in ogni suo punto una distribuzione uniforme del suo peso totale, essa è stata spesso utilizzata per realizzare manufatti e strutture architettoniche. Le strutture realizzate secondo tale curva subiscono soltanto sforzi a trazione, come le funi di sostegno nei ponti sospesi, oppure, in alternativa, a compressione, quando la struttura realizzata ha la forma di una catenaria rovesciata, come nelle strutture di cupole. Ne sono un esempio la cupola della cattedrale di St. Paul a Londra (a sinistra), progettata da Robert Hooke (colui che studiò le leggi dell´elasticità) e la Sagrada Familia a Barcellona (al centro), progettata da Gaudì. Inoltre numerosi ponti sono realizzati con la struttura di una catenaria rovesciata tra cui ricordiamo il famoso ponte di Santa Trinita a Firenze (immagine in basso). Infine citiamo il famoso Gateway Arch (a destra) dell´architetto finlandese Saarinen, posto nel parco del Jefferson National Expansion Memorial.