Esempio

Esempio 1

Studiare la parabola $\mathcal{C}:y=3x^{2}+2x-3$ .
Soluzione 1
Riscriviamo l'equazione nel modo seguente (metodo del completamento dei quadrati):

$\begin{displaymath} \displaystyle y=3\left(x^2+\frac{2}{3}x+\frac{1}{9}\right)-3-\frac{1}{3} \end{displaymath}$

$\begin{displaymath} \left(y+\frac{10}{3}\right)=3\left(x+\frac{1}{3}\right)^2 \end{displaymath}$

con la traslazione

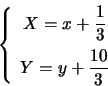
$\begin{displaymath} \left \{ \begin{array}{c} X=x+\displaystyle\frac{1}{3}\vs... ...{2mm}\\ Y=y+\displaystyle\frac{10}{3} \end{array} \right. \end{displaymath}$

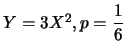
l'equazione diventa $Y=3X^2,p=\displaystyle\frac{1}{6}$

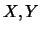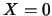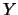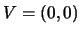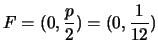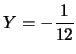
Rispetto alle coordinate l'asse è (asse ), il vertice è , il fuoco è $F=(0,\displaystyle\frac{p}{2})=(0,\displaystyle\frac{1}{12})$ , la direttrice è $Y=-\displaystyle\frac{1}{12}$
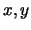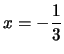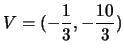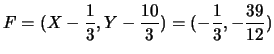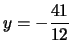
Rispetto agli assi l'asse è $x=-\displaystyle\frac{1}{3}$ , il vertice è $V=(-\displaystyle\frac{1}{3},-\displaystyle\frac{10}{3})$ , il fuoco è $\displaystyle F=(X-\frac{1}{3},Y-\frac{10}{3})=(-\frac{1}{3},-\frac{39}{12})$ , la direttrice è $y=-\displaystyle\frac{41}{12}$

Soluzione 2
Poichè coefficienti di una parabola con l'asse asse di simmetria basterà applicare le formule () per pervenire agli stessi risultati.