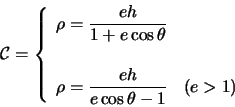Equazione polare dell'iperbole.
Consideriamo un'iperbole di fuoco 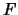 e direttrice
e direttrice 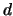 .
.
Fissiamo un sistema di riferimento 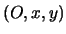 ortonormale in modo che:
ortonormale in modo che:
- 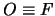
- l'asse 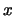 sia orientato da
sia orientato da 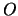 verso
verso 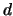 .
.
Sia ora 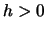 la distanza tra
la distanza tra 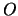 e il punto di intersezione tra
e il punto di intersezione tra
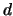 e l'asse
e l'asse 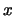 ,
, 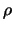 la lunghezza del vettore
la lunghezza del vettore
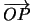 ,
, 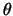 è l'angolo che
è l'angolo che
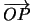 forma con l'asse x.
forma con l'asse x.
Figura:
Il punto P è sull'iperbole.
|
|
Si ha 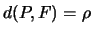 e
e
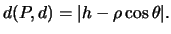 Sostituendo a
Sostituendo a
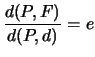 si ottiene
si ottiene
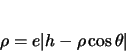 |
(4) |
Distinguiamo ora due casi:
Il secondo caso è possibile solo se 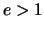
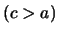 .
.
Quindi si ottiene
che sono le equazione dei due rami di iperbole. Tale equazione è
detta equazione polare dell'iperbole.
![\includegraphics[width=12cm,height=8.5cm]{i-polare}](img11.png)
![]() e
e
![]() Sostituendo a
Sostituendo a
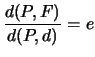 si ottiene
si ottiene