Dimostrazione
Denotiamo con 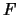 ,
, 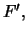 rispettivamente,
i due fuochi. Fissiamo un sistema cartesiano
rispettivamente,
i due fuochi. Fissiamo un sistema cartesiano 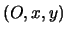 tale che
l'asse
tale che
l'asse 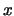 passi per
passi per
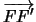 e l'origine sia il
punto medio del segmento
e l'origine sia il
punto medio del segmento
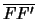 . Allora i due fuochi
avranno coordinate
. Allora i due fuochi
avranno coordinate 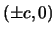 . Il punto
. Il punto 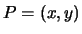 verifica la
condizione
verifica la
condizione
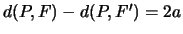 se e solo se
se e solo se
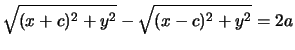 ,
da cui segue
,
da cui segue
e si arriva infine all'identità
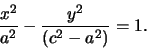 |
(3) |
Adesso consideriamo il triangolo 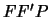
(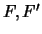 fuochi,
fuochi, 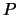 punto sull'iperbole).
punto sull'iperbole).
Poichè in un triangolo la differenza, in valore assoluto, tra due
lati è minore del terzo abbiamo
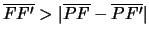 cioè
cioè
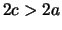 da cui
da cui 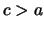 . Possiamo allora porre
. Possiamo allora porre
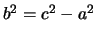 ,
e la (
,
e la (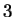 ) rappresenta l'equazione canonica
dell'iperbole.
) rappresenta l'equazione canonica
dell'iperbole.
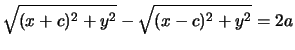 ,
da cui segue
,
da cui segue