Se gli asintoti sono tra loro ortogonali (cioč se ![]() )
l'iperbole si dice equilatera.
)
l'iperbole si dice equilatera.
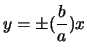 (cioč le uniche rette
che passano per l'origine e non intersecano
(cioč le uniche rette
che passano per l'origine e non intersecano
Se gli asintoti sono tra loro ortogonali (cioč se ![]() )
l'iperbole si dice equilatera.
)
l'iperbole si dice equilatera.
Osservazione 2
Le rette
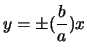 sono asintoti per
entrambe le funzioni (
sono asintoti per
entrambe le funzioni (![]() ).
).
Per asintoti intendiamo:
Sia ![]() una funzione continua in
una funzione continua in ![]() La retta di
equazione
La retta di
equazione ![]() si dice asintoto di
si dice asintoto di ![]() , per
, per
![]() , se
, se
| Dimostrazione Osservazione 2 |
Nella figura č messo in evidenza il significato geometrico dei
numeri ![]() . I due asintoti costituiscono le diagonali del
rettangolo di lati
. I due asintoti costituiscono le diagonali del
rettangolo di lati ![]() e
e ![]() .
.
| Esempio | Osservazioni |