Dimostrazione
Sia 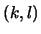la segnatura di 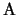, matrice che rappresenta la conica nella forma (). .
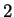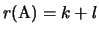Possiamo assumere .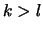
Poichè 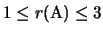andiamo a distinguere ciascun caso.

.

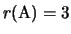• La segnatura è 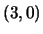, in un opportuno sistema di riferimento l'equazione diventa 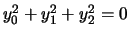. Tale equazione non ha soluzioni in e rappresenta una conica generale a punti non reali.
• La segnatura è , l'equazione diventa 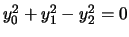, che è l'equazione di una conica generale.

.

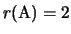• La segnatura è 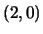, l'equazione diventa 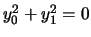.Conica semplicemente degenere. Poich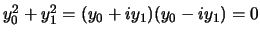è si dice che la conica è l'unione di due rette complesse e coniugate.
• La segnatura è 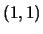, l'equazione diventa 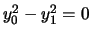. Conica semplicemente degenere. Poich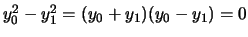è si dice che la conica è unione di due rette distinte.

.

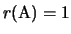• La segnatura è 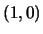e l'equazione divent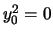a , ossia una retta doppia.