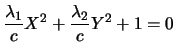Dimostrazione Teorema 1

Dimostrazione

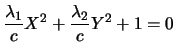Consideriamo l'equazione (). Se $c\neq 0,$ dividiamo() per c ed abbiamo $\displaystyle\frac{\lambda_1}{c}X^2+\frac{\lambda_2}{c}Y^2+1=0$ .

Distinguiamo tre casi:

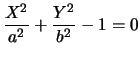Se $\displaystyle\frac{\lambda_1}{c}$ e $\displaystyle\frac{\lambda_2}{c}$ sono entrambi negativi si ottiene $\displaystyle\frac{X^2}{a^2}+\frac{Y^2}{b^2}-1=0$ che è l'equazione canonica di un ellisse.
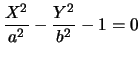Se $\displaystyle\frac{\lambda_1}{c}$ e $\displaystyle\frac{\lambda_2}{c}$ sono di segno opposto si ottiene $\displaystyle\frac{X^2}{a^2}-\frac{Y^2}{b^2}-1=0$ che è l'equazione canonica di un iperbole.
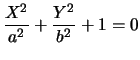Se $\displaystyle\frac{\lambda_1}{c}$ e $\displaystyle\frac{\lambda_2}{c}$ sono positivi si ottiene l'equazione $\displaystyle\frac{X^2}{a^2}+\frac{Y^2}{b^2}+1=0$ che non ha soluzioni reali. Da qui il nome di ellisse a punti non reali o ellisse immaginaria.

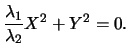si ha l'equazione $\displaystyle\frac{\lambda_1}{\lambda_2}X^2+Y^2=0.$ Distinguiamo due casi:

Se $\lambda_1$ e $\lambda_2$ hanno segno opposto la () diventa . Se fattorizziamo tale equazione otteniamo ; la conica quindi è data dall'unione delle rette di equazione $Y=\pm aX$ . Abbiamo così l'equazione di due rette reali incidenti in punto.

Figura: Con l'equazione nella forma canonica, il punto di incidenza delle due rette corrisponde all'origine degli assi.

$\includegraphics[width=7.5cm,height=9cm]{retteincidenti.ps}$

**Figura:** Con l'equazione nella forma canonica, il punto di incidenza delle due rette corrisponde all'origine degli assi.
$\includegraphics[width=7.5cm,height=9cm]{retteincidenti.ps}$

Se $\lambda_1$ e $\lambda_2$ hanno lo stesso segno abbiamo invece che ammette una sola soluzione reale, per . Tale polinomio infatti non è riducibile in $\mathbf R$ e può essere fattorizzato nel prodotto di due polinomi di primo grado nel campo complesso ; la conica quindi è data dall'unione di due rette di equazione $Y=\pm iaX$ .
L'equazione rappresenta una coppia di rette complesse coniugate incidenti in un punto reale, l'origine degli assi.

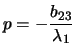Per quanto riguarda l'equazione () è sufficiente porre $\displaystyle p=-\frac{a'_{23}}{\lambda_1}$ e, scambiando X con Y, si ha l'equazione canonica di una parabola.

Resta soltanto l'equazione ()

Se si ottiene l'equazione , cioè una retta contata due volte. Se rappresenta ancora l'asse Y, l'equazione rappresenta l'asse ma con molteplicità .

Figura: l'asse con molteplicità 2.

$\includegraphics[width=7.5cm,height=9cm]{retteassi.ps}$
Se $d\neq 0$ ( $\lambda_1\neq 0$ ) .

**Figura:** l'asse con molteplicità 2.
$\includegraphics[width=7.5cm,height=9cm]{retteassi.ps}$

Se $\displaystyle\frac{d}{\lambda_1}<0$ allora, posto $\displaystyle a^2=\frac{d}{\lambda_1}$ otteniamo . Se fattorizziamo questo polinomio nel prodotto di due polinomi di primo grado otteniamo . La conica è data dall'unione di due rette parallele all'asse delle Y che intersecano l'asse delle X rispettivamente nei punti . La conica è costituita da due rette parallele e distinte.

**Figura:** Rette parallele
$\includegraphics[width=7.5cm,height=9cm]{retteparallele.ps}$

Se $\displaystyle\frac{d}{\lambda_1}>0$ , ponendo si ottiene . Che non ha soluzioni reali ma in $\mathbf C$ , si fattorizza come . La conica quindi è data dall'unione di due rette complesse e coniugate parallele e distinte.